sviluppo Risolvere il seguente problema In un triangolo rettangolo un cateto l'ipotenusa supera un cateto di 6 cm; sapendo che l'altro cateto vale 12 cm. determinare il perimetro del triangolo ipotesi: il triangolo e' rettangolo; l'ipotenusa supera un cateto di 6 cm l'altro cateto vale 12 cm tesi: trovarne il perimetro cioe' primo cateto + secondo cateto + ipotenusa 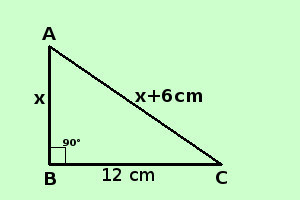Perimetro = primo cateto + secondo cateto + ipotenusa lunghezza del primo cateto = AB = x lunghezza del secondo cateto = BC = 12 cm lunghezza dell'ipotenusa = AC = x + 6 cm Per trovare il perimetro devo trovare le misure del cateto e dell'ipotenusa; non ho una relazione risolvente ma so che il triangolo e' rettangolo quindi applico il Teorema di Pitagora al triangolo (posso farlo perche' e' un triangolo rettangolo) posso esprimerlo come il quadrato del primo cateto piu' il quadrato del secondo cateto e' uguale al quadrato dell'ipotenusa     x2 + 122 = (x + 6)2 Calcolo    x2 + 144 = x2 + 12x + 36 porto i termini con la x prima dell'uguale, quelli senza dopo l'uguale, chi salta l'uguale cambia di segno     x2 - x2 - 12x = 36 - 144 sommo i termini simili     - 12x = - 108 applico il secondo principio per trovare la x     -12x -12   =   -108 -12     x = 9 lunghezza del primo cateto = AB = x = 9 lunghezza del secondo cateto = BC = 12 lunghezza dell'ipotenusa = AC = x + 6 = 15 Perimetro = primo cateto + secondo cateto + ipotenusa = 9 + 12 + 15 = 36 cm E' buona norma controllare sempre che, grosso modo, le dimensioni relative nella figura fatta corrispondano al risultato (cioe' in questo caso che le misure del primo cateto, del secondo e dell'ipotenusa si corrispondano alla figura)