sviluppo
Risolvere il seguente sistema
Il sistema deve essere ridotto a forma normale: eseguiamo le operazioni indicate:
moltiplico per eliminare le parentesi tonde
 |
1

8 |
x - |
1

4 |
y = |
1

5 |
x - |
1

5 |
z |
|
|
|
|
|
faccio il m.c.m. nella prima e terza equazione; nella seconda porto il termine con l'incognita z prima dell'uguale
 |
5x - 10y

40 |
= |
8x - 8z

40 |
|
|
|
3x - 2y - 2z

6 |
= |
18

6 |
|
tolgo i denominatori
 |
5x - 10y = 8x - 8z |
| x + 4y - 2z = -2 |
| 3x - 2y - 2z = 18 |
porto i termini con le incognite prima dell'uguale
 |
5x - 10y - 8x + 8z = 0 |
| x + 4y - 2z = -2 |
| 3x - 2y - 2z = 18 |
sommo i termini simili
 |
3x + 10y - 8z = 0 |
| x + 4y - 2z = -2 |
| 3x - 2y - 2z = 18 |
utilizziamo il metodo di Cramer applicando poi la regola di Sarrus per calcolare i determinati di ordine 3

 |
3 |
10 |
-8 |
0 |

 |
| 1 |
4 |
-2 |
-2 |
| 3 |
-2 |
-2 |
18 |
| x = |
 |
0 |
10 |
-8 |
 |
= |
| -2 |
4 |
-2 |
| 18 |
-2 |
-2 |
 |
 |
3 |
10 |
-8 |
 |
| 1 |
4 |
-2 |
| 3 |
-2 |
-2 |
| y = |
 |
3 |
0 |
-8 |
 |
= |
| 1 |
-2 |
-2 |
| 3 |
18 |
-2 |
 |
 |
3 |
10 |
-8 |
 |
| 1 |
4 |
-2 |
| 3 |
-2 |
-2 |
| z = |
 |
3 |
10 |
0 |
 |
= |
| 1 |
4 |
-2 |
| 3 |
-2 |
18 |
 |
 |
3 |
10 |
-8 |
 |
| 1 |
4 |
-2 |
| 3 |
-2 |
-2 |
Calcolo il determinante ai denominatori (i denominatori sono tutti uguali, quindi lo calcolo prima)
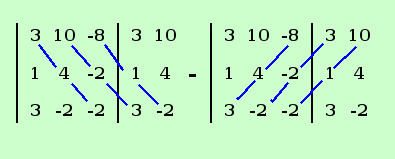 |
= 3·4·(-2) + 10·(-2)·3 -8·1·(-2) -3·4·(-8) - (-2)·(-2)·3 -(-2)·1·10 =
= -24 - 60 + 16 + 96 - 12 + 20 = 36 |
Calcolo il determinante al numeratore della x
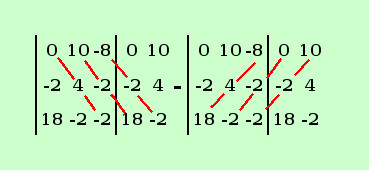 |
= 0 + 10·(-2)·18 -8·(-2)·(-2) - 18·(4)·(-8) + 0 - (-2)·(-2)·10 =
= -360 - 32 + 576 - 40 = 144 |
quindi
| x = |
144

36 |
= 4 |
Calcolo il determinante al numeratore della y
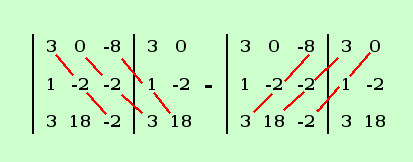 |
= 3·(-2)·(-2) + 0 - 8·1·18 -3·(-2)·(-8) -18·(-2)·3 -0 =
= 12 -144 - 48 + 108 = -72 |
quindi
| y = |
-72

36 |
= -2 |
Calcolo il determinante al numeratore della z
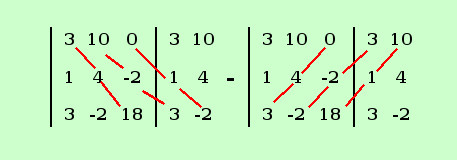 |
=3·4·18 + 10·(-2)·3 +0 -0 -(-2)·(-2)·3 -18·1·10 =
= 216 -60 +12 -180 = 12
|
quindi
| z = |
12

36 |
= |
1

3 |
otteniamo
 |
x = 4 |
| y = -2 |
| z = 1/3 |
|



