|
Un mio amico, matematico con la passione per la fisica mi ha fatto notare che se prendo una corda di 40.000.000 di metri (quaranta milioni di metri) posso, stendendola a terra, circondare la terra tutto attorno all'equatore Se sollevo la corda di un metro , per poter fare il giro della terra sull'equatore devo allungarla di metri 6 e 28 centimetri Infatti siccome la misura della circonferenza e' 2πr per trovare la misura della circonferenza della corda rialzata basta fare 2π(r+1)=2πr + 2π = circonferenza iniziale +6,28 metri questo per dirti che spesso le cose sono strane; solo mediante il ragionamento matematico possiamo avere una ragionevole certezza della loro realta' Tra tutte le stranezze, comunque, il posto d'onore spetta al concetto di infinito che sara' ampiamente usato in analisi matematica Fissiamo subito una cosa fondamentale:
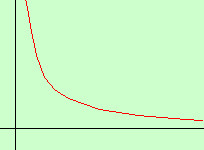
Man mano che x cresce il valore della y diminuisce e la curva, quindi il punto si avvicina all'asse delle x dopo mille metri la distanza sara' di 1/1000m = 1 millimetro dopo un milione di metri la distanza sara' 1/1000000m = 1 µ (micron) dopo mille miliardi di metri la distanza fra la curva e l'asse x sara' minore del diametro di un atomo.. e posso proseguire mentalmente posso arrivare ad una distanza dall'origine pari o superiore al diametro dell'intero universo ed ancora, per la mia mente, la curva e l'asse x hanno ancora una distanza Quindi tale distanza sara' inferiore al diametro di un atomo, al diametro di un protone, alla dimensione di un quark, alla lunghezza di una stringa,..... quindi che senso ha parlare di distanza? Per poter salvare capra e cavoli allora parlo di infinito ed infinitesimo, nel senso che posso sempre andare avanti e trovero' ancora numeri per x ma a zero non ci arrivero' mai. Diremo quindi che per x tendente ad infinito la distanza fra la curva e l'asse x tende a zero, od anche che la curva e l'asse x hanno in comune un punto all'infinito
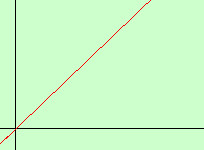
Man mano che x cresce il valore della y aumenta dopo mille metri l'altezza sara' di 1000m dopo un milione di metri la distanza sara' un milione di metri dopo mille miliardi di metri presi sull'asse x la distanza fra la curva e l'asse x sara' mille miliardi di metri.. e posso proseguire mentalmente posso arrivare ad una distanza dal punto all'asse delle x pari o superiore al diametro dell'intero universo ed ancora, per la mia mente, il punto puo' ancora procedere sulla curva quindi anche qui che senso ha parlare di distanza?Allora parlo di infinito, nel senso che posso sempre andare avanti e trovero' sempre ancora numeri Diremo quindi che per x tendente ad infinito anche y, cioe'la distanza fra la curva e l'asse x, tende ad infinito prima di procedere ti propino una vecchia barzelletta che ti chiarira' meglio il concetto Gara mondiale fra matematici a chi riesce a scandire il numero Naturale piu' grande dopo alcuni contendenti arriva il super matematico A che comincia a scandire; "Un miliardo di miliardi, di miliardi, di miliardi, di miliardi, di miliardi, di miliardi,...." e continua cosi' per ore con uno sforzo tremendo finche' con le ultime forze pronuncia " di miliardi, di miliardi, di miliardi, di miliardi, di miliardi, di miliardi" poi si accascia svenuto per lo sforzo Allora il matematico B si alza ed urla; " piu' uno!" Grande boato di folla, viene acclamato subito vincitore e portato in trionfo fuori dai presenti. In sala resta il matematico C che piange e si dispera, a chi gli chiede perche' pianga risponde: "Piango perche' non ho detto piu' due, sarei io il vincitore!" A parte la barzelletta scema il concetto di infinito e' proprio questo: ce n'e' sempre uno in piu'! Quindi per misurare l'infinito cosa e' meglio se non utilizzare l'insieme dei numeri naturali che si ottengono l'uno dall'altro aggiungendo 1? Assiomi di Peano per la generazione dell'insieme N a partire da 1
Per questo utilizzeremo la definizione: un insieme e' infinito se un qualunque suo sottoinsieme puo' essere posto in corrispondenza biunivoca con l'insieme dei numeri naturali Ad ogni numero naturale corrisponde un punto del sottoinsieme e viceversa ad ogni punto del sottoinsieme corrisponde un numero naturale E' un concetto che abbiamo gia' trovato: Un punto e' di accumulazione per un insieme se preso comunque un intorno del punto stesso al suo interno esiste sempre un altro punto appartenente all'insieme Significa che posso sempre aggiungere un punto ed aggiungendo un punto per volta ottengo infiniti punti, il che mi porta alla definizione Un punto e' di accumulazione per un insieme se preso comunque un intorno del punto stesso al suo interno esistono infiniti punti appartenenti all'insieme Altra definizione che abbiamo ncontrato intervallo continuo significa che presi comunque due punti dell'intervallo diversi fra loro in mezzo trovero' sempre un terzo punto Significa che posso sempre aggiungere un punto ed aggiungendo un punto per volta ottengo infiniti punti fra i due considerati Vediamo adesso quali tipi di infinito ci interessano: c'e' l'infinito asintotico (primo esempio con l'iperbole equilatera si dice asintoto la tangente alla curva all'infinito l'infinito illimitato (secondo esempio con la bisettrice del primo e terzo quadrante, c'e' anche l'infinito limitato (sembra quasi un ossimoro) ossimoro e' una contraddizione in termini come ad esempio "diavol di un angelo!" Infinito limitato Se ad esempio considero il segmento di retta reale I = { x ∈ ℜ / 1 < x ≤ 5} tale segmento quanti punti contiene? Evidentemente infiniti, infatti posso pensare ogni suo punto come finale di un suo sottoinsieme in corrispondenza biunivoca con l'insieme N se ad esempio prendo 3, posso prendere come insieme infinito
2,9 2,99 2,999 2,9999 2,99999 2,999999 ........ →3 Diremo quindi che per k tendente ad infinito la successione tende a 3, od anche che 3 e' il limite della successione per k tendente all'infinito e questo posso farlo per ogni suo punto sia interno che di frontiera Un tipo di infinito di questo genere e' detto limitato, perche' puo' essere completamente contenuto in un intervallo chiuso di ℜ, nel nostro caso basta che prendi l'intervallo da 0 a 6 se vuoi approfondire torna agli esercizi precedenti |
|||||||||||||||
|
|
|
|