|
Pero' questa ti fornisce un metodo generale per operare sempre la scomposizione sui polinomi ordinati, se cio' non e' possibile diremo che il polinomio non e' scomponibile. Partiamo da un polinomio molto semplice, ad esempio consideriamo x2+5x+6 il problema che ci poniamo e' trovare due polinomi che moltiplicati mi diano come risultato il polinomio di partenza. Si pensa che il polinomio abbia come fattore un fattore del tipo (x-a) in cui a e' un numero Quindi possibili fattori potranno essere: (x-1) (x+1) (x-2) (x+2) (x-3) (x+3) ...... Si tratta di vedere se questi sono effettivamente fattori oppure no. Ricordando che un termine e' fattore di un secondo termine se il primo divide esattamente il secondo (cioe' il resto della divisione vale 0) dovremo fare (x2+5x+6):(x-1) e calcolarne il resto. se viene 0 e' un fattore altrimenti proveremo (x2+5x+6):(x+1) poi (x2+5x+6):(x-2) finche' non troviamo il resto 0 Ricordiamo che per trovare il resto possiamo applicare il teorema di Ruffini quindi troviamo i possibili resti Troviamo il resto dividendo (x2+5x+6)per (x-1) (x-1); P(1)=12+5(1)+6 =1+5+6=12 diverso da 0 proviamo ora (x+1); P(-1) = (-1)2+5(-1)+6 = 1-5+6 = 2 diverso da 0 (x-2); P(2)=22+5(2)+6 = 4+10+6 = 20 diverso da 0 (x+2); P(-2)=(-2)2+5(-2)+6 = 4-10+6 = 0 allora (x+2) e' un fattore Quindi potremo scrivere (x2+5x+6) = (x+2)·(qualcosa) Per trovare cos'e' quel qualcosa facciamo il seguente ragionamento: 4e' un fattore di 20 ed io posso scrivere 20 = 4·(qualcosa) quanto vale quel qualcosa? 5 ; e come ho fatto ad ottenerlo? Evidentemente facendo 20:4 Facciamo quindi nello stesso modo: per trovare l'altro fattore eseguiamo (x2+5x+6):(x+2) = e naturalmente utilizziamo la divisione di Ruffini 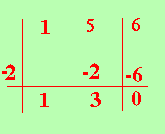
quindi (x2+5x+6) = (x+2)(x+3) Proviamo un'altra scomposizione: x3-x2 -5x-3 = Proviamo se il resto e' nullo quando dividiamo per x-1 (x-1): P(1) = (1)3-(1)2 -5(1)-3 = 1-1-5-3 = -8 diverso da zero proviamo ora per x+1 (x+1): P(-1) = (-1)3-(-1)2 -5(-1)-3 = -1-1+5-3 = 0 questo e' un divisore, quindi scrivo x3-x2 -5x-3 = (x+1)·qualcosa Per trovare cosa devo mettere al posto di qualcosa faccio la divisione di Ruffini 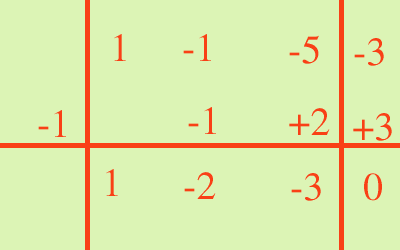
quindi ottengo x3-x2 -5x-3=(x+1)·(x2-2x-3) non e' finita: devo ancora scomporre la parte fra parentesi (x2-2x-3) perche' e' di grado superiore al primo ricomincio con Ruffini ma non provo x-1 perche' se non andava bene per tutto il polinomio non andra' bene nemmeno per una sua parte; quindi ricomincio dall'ultimo che mi ha dato il risultato giusto, perche' un fattore puo' essere ripetuto:esempio 12=2X2X3 (x+1): P(-1)= (-1)2 -2(-1)-3=1+2-3=0 questo e' un divisore, quindi scrivo x3-x2 -5x-3=(x+1)·(x2-2x-3)=(x+1)·(x+1)·qualcosa Rifaccio la divisione 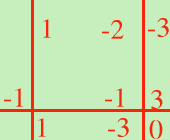 quindi x3-x2 -5x-3=(x+1)·(x2-2x-3)=(x+1)·(x+1)·(x-3) Uno degli errori piu' comuni facendo la divisione e' scrivere: x3-x2 -5x-3=(x+1)·(x2-2x-3)=(x+1)·(x-3) Sarebbe come scrivere 12=2x6=2x3; e' un errore perche' 2x3 non e' uguale a 12 cioe' facendo la moltiplicazione l'ultimo termine deve sempre tornare uguale al primo, quindi devo sempre ripetere tutti i fattori Avete visto che la divisione e' un'operazione piuttosto difficile da fare, allora cerchiamo qualche "trucco" per poter abbreviare qualcosa: trucco 1: Limitare il numero dei fattori Prima di tutto notiamo che nelle scomposizioni gia' fatte: x2+5x+6=(x+2)(x+3) x3-x2 -5x-3=(x+1)·(x+1)·(x-3) il termine senza la lettera del polinomio di partenza e' il prodotto dei termini noti dei fattori cioe': nel primo 6=2·3 nel secondo -3=1·1·(-3) ma allora se devo ad esempio scomporre x2-10x+21 21 sara' il prodotto dei termini noti dei binomi che mi scompongono il polinomio quindi non dovro' provare tutti i fattori ma solamente P(1) P(-1) P(3) P(-3) P(7) P(-7) P(21) P(-21) Sara' inutile provare ad esempio P(2) perche' moltiplicando 2 per un intero non posso avere come risultato 21 trucco 2: mettere i segni giusti E' da applicare ai segni quando vado a calcolare P(1), P(-1), P(2), P(-2) ecc Se vado a calcolare P(1), P(2), P(3), P(4) ..i segni dei termini non cambieranno perche' il numero che sostituisco al posto della x e' positivo, quindi dove c'e' piu' resta piu' e dove c'e' meno resta meno Se invece vado a calcolare P(-1), P(-2), P(-3), P(-4) .. resteranno uguali i segni dei termini a potenza pari mentre cambieranno i segni per le potenze dispari ora bisogna trattare quelli che io chiamo i casi patologici |

|

|

|

|