Caso del polinomio non completo Succede abbastanza spesso che il polinomio non sia completo, cioe' che manchino dei termini ad esempio proviamo a scomporre: x3-2x +1 provo (x-1); P(1)=(1)3-2(1)+1=1-2+1=0 quindi (x-1) e' un divisore, pero' posso fare la divisione di Ruffini solo se ci sono tutti i termini ed allora siccome mi manca x2 al suo posto dovro' mettere uno zero cioe' x3+0x2-2x +1 ed ora procedo nel solito modo: 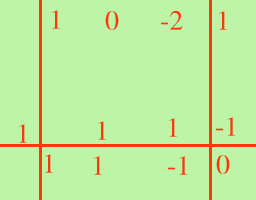quindi x3-2x +1=(x-1)(x2 +x-1) Ora si dovrebbe scomporre x2+x-1 provo (x-1); P(1)=(1)2+(1)-1=1+1-1≠0 (x+1); P(-1)=(-1)2+(-1)-1=1-1-1≠0 e poiche' i divisori del termine noto sono solamente +1, -1 il polinomio non e' ulteriormente scomponibile: risultato finale: x3-2x +1=(x-1)(x2 +x-1) Per esercizio prova a scomporre x5-32= ricordando che per ordinare dovrai scrivere x5+0x4 +0x3+0x2+0x-32=