|
xn + an per n dispari, cioe' ad esempio x3 + a3 = x5 + a5 = x7 + a7 = .......... dove al posto di a possiamo pensare un numero; per trovare la regola di scomposizione proviamo a scomporre con Ruffini e vediamo se riusciamo ad individuare delle regolarita' come nella schermata precedente Iniziamo a scomporre x3 + a3 = essendo il termine noto a3 il possibile divisore di Ruffini sara' del tipo (x-a); (x+a) Provo a dividere per (x-a) (x-a) ; P(a)=a 3+ a3 ≠0 (x+a) ; P(-a)=(-a) 3+ a3 =-a3+ a3 =0 Essendo il resto zero (x+a) e' un divisore; eseguo la divisione 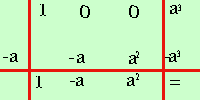 ottengo x3 + a3 = (x+a)(x2-ax+a2) Proviamo ora a scomporre x5 + a5 = (x-a) ; P(a)=a 5+ a5 ≠0 (x+a) ; P(-a)=(-a) 5+ a5 = -a 5+ a5 =0 Essendo il resto zero (x+a) e' un divisore; eseguo la divisione 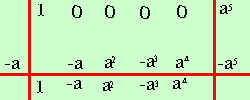 ottengo x5 + a5 = (x+a) (x4 -ax3 +a2x2 -a3x +a4) Ora senza eseguire Ruffini ma tenendo presenti le due scomposizioni x3 + a3 = (x+a) (x2-ax+a2) x5 + a5 = (x+a) (x4 -ax3 +a2x2 -a3x +a4) Voglio scomporre x7 + a7 = Intanto il divisore sara' (x+a) x7 + a7 = (x+a) (.....) osserviamo che dentro parentesi al posto dei puntini devo mettere il primo termine abbassato di un grado, cioe' x6 poi man mano devo fare un polinomio ordinato abbassando la potenza della x ed aumentando la potenza della a ed i segni sono alternati: uno positivo e l'altro negativo .. quindi x7 + a7 = (x+a) (x6 -ax5 +a2x4 -a3x3 +a4x2 -a5x +a6) Regola: una somma di potenze dispari e' uguale al prodotto di un binomio dato dalla somma delle basi per un polinomio ordinato e completo ottenuto abbassando di un grado il primo termine, poi via via abbassando di un grado il primo ed aumentando di un grado il secondo ed i segni sono alternati Per esercizio prova a scomporre: x9 + a9 = poi controlla il risultato |

|

|

|

|