discussione di equazioni di primo grado metodo grafico Consideriamo la corrispondenza (fare link a significato geometrico di un sistema) fra l'equazione di primo grado ax+b=0 ed il sistema y = ax + b y = 0 questo si puo' rappresentare graficamente come una retta che taglia l'asse delle x nel punto che corrisponde alla soluzione dell'equazione Essendo la nostra equazione con un parametro avremo che potremo rappresentare il sistema come un fascio di rette. La discussione si ridurra' a vedere quali rette del fascio risolvono la condizione richiesta, cioe' quali rette hanno l'intersezione con l'asse delle x a destra od a sinistra del valore dato Vediamo lo stesso esempio gia' fatto Discutere l'equazione 2x + k - 1 = 0 rispetto alla condizione x > 2 Considero la funzione y = 2x + k - 1 Questa rappresenta un fascio di rette parallele perche' al variare di k varia il termine noto mentre il coefficiente angolare e' fisso e vale 2 nel sistema y = 2x + k - 1 y=0 sostituisco a x il valore 2 e trovo il corrispondente valore di k k = -3 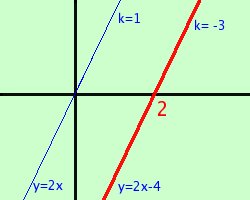Faccio il grafico riportando le rette del fascio; disegno prima la retta passante per l'origine y=2x (basta togliere il termine noto) calcolo il suo valore di k (termine noto k-1=0 cioe' k=1) disegno ora quella con k=-3 cioe' la parallela passante per x=2, avra' equazione y=2x-4 ora siccome devo prendere i valori per x > 2 cioe' le rette che intersecano l'asse delle x a destra del punto 2 allora avro' la soluzione k < -3 perche' essendo k=1 per la retta passante per l'origine e k=-3 per la retta di base avro' che procedendo verso destra il valore di k diventera' sempre piu' piccolo (nel senso che raggiungera' valori negativi sempre piu' alti) Come vedi non e'che la discussione di un'equazione di primo grado sia troppo gratificante, anzi direi proprio il contrario potremmo far vedere cosa succede se il fascio di rette e' proprio, cioe' se k e' moltiplicato per la x nell'equazione, ma in pratica non cambia granche'; lo faro' nella seconda stesura del sito