|
Qui devi essere abbastanza "esperto" di geometria cartesiana: il problema si puo' scomporre di solito nell'intersezione o fra una retta ed una parabola, oppure fra due parabole, od anche, soprattutto nei problemi trigonometrici nell'intersezione fra una retta ed una circonferenza: una delle due, possibilmente la retta, variera' al variare del parametro k, intersecando l'altra curva in uno, nessuno o due punti.Queste intersezioni nelle parti di figura comprese nei limiti, forniranno le soluzioni Per ora ci limiteremo ad un semplice esempio, rimandando alla seconda stesura del sito lo studio dei vari casi possibili discutere al variare del parametro k l'equazione x2 - 3x + 2k - 1 = 0 con i limiti -2 < x  4 qui siamo abbastanza liberi: dobbiamo trasportare dopo l'uguale una parte dell'equazione in modo da avere l'uguaglianza fra due curve note di cui una fissa (cioe' una senza il parametro) i punti comuni alle due curve nei limiti richiesti saranno le soluzioni cercate potrei prendere x2 - 3x - 1 = - 2k la parabola fissa y = x2 -3x -1 con la retta variabile y= - 2k x2 - 3x = 1 - 2k la parabola fissa y = x2 - 3x con la retta variabile y= 1 - 2k x2 = 3x + 1 - 2k la parabola fissa y = x2 con la retta variabile y = 3x + 1 - 2k x2 + 2k = 3x + 1 la parabola variabile y = x2 + 2k con la retta fissa y = 3x + 1 x2 + 2k -1 = 3x la parabola variabile y = x2 + 2k - 1 con la retta fissa y = 3x x2 - 3x + 2k = 1 la parabola variabile y = x2 - 3x + 2k con la retta fissa y = 1 Prendiamo quella che ci sembra piu' semplice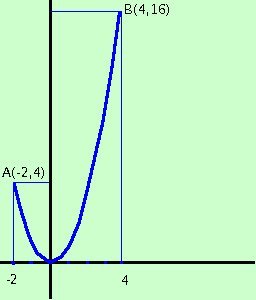 
x2 = 3x + 1 - 2k la parabola fissa y = x2 con la retta variabile y = 3x + 1 - 2k 
y = x2 y = 3x + 1 - 2k Disegniamo la curva y = x2 : e' una parabola con il vertice nell'origine e prendiamone solo la parte che ci interessa, cioe' per -2 < x  4
Troviamo i valori al limite sostituendo nella x della parabola i valori limite: otteniamo i punti A(-2,4) B(4,16)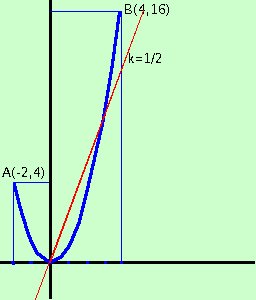 
adesso prendiamo la retta
y = 3x + 1 - 2k; notiamo che varia solamente il termine noto; quindi l'equazione rappresenta un fascio di rette parallele. Cominciamo col disegnare la retta del fascio che passa per l'origine
y = 3x e mettiamola nel grafico; ad essa corrisponde il valore di k : (termine noto = 0) 1 - 2k = 0 k = 1/2 non sarebbe necessario fare il passaggio per l'origine ma ti puo' aiutare a capire meglio il problema: adesso devi pensare di spostare la retta parallelamente a se' stessa in modo che passi per il punto A, per il punto B e per il punto di tangenza e contare quante sono le intersezioni con l'arco di parabola nella prossima figura prendo solo le rette necessarie Facciamo il passaggio per il punto A(-2,4) e troviamo il valore di k: basta sostituire nella retta ad x il valore -2 e ad y il valore 4 4 = 3(-2) + 1 - 2k 4 = -5 - 2k 2k = - 9 k= - 9/2 Facciamo il passaggio per il punto B(4,16) e troviamo il valore di k: basta sostituire nella retta ad x il valore 4 e ad y il valore 16 16 = 3(4) + 1 - 2k 16 = 13 - 2k 2k = -3 k= - 3/2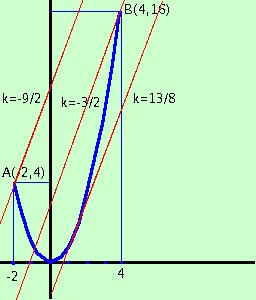 
Troviamo ora il valore di k quando la retta e' tangente: bastera' risolvere il sistema tra la retta e la parabola (cioe' prendere l'equazione iniziale) e porre il discriminante uguale a zerox2 - 3x + 2k - 1 = 0 a = 1 b = -3 c = 2k -1 b2 - 4ac = 0 (-3)2 - 4(1)(2k-1) = 0 9 - 8k + 4 = 0 -8k = -13 k = 13/8 quindi abbiamo Una soluzione per - 9/2 < k < - 3/2 Due soluzioni per -3/2 k 13/8 Per i segni di minore e di minore uguale, siccome abbiamo -2 < x 4 il punto B e' da considerare valido per la soluzione, mentre il punto A non da' soluzioni
|
|
|
|
|