|
Per poterle risolvere devi conoscere la rappresentazione cartesiana della retta nel piano vedere Avremo le due incognite x ed y a potenza 1 Ad esempio: 3x - 2y - 3 e' una disequazione di primo grado in due incognite Tieni sempre presente, se devi fare una moltiplicazione, la regola vista nella pagina precedente Porto tutti i termini prima dell'uguale; chi salta l'uguale cambia di segno. 3x - 2y - 3 - 2x + y + 2 calcolo x - y - 1 Considero la funzione x - y - 1 = 0: 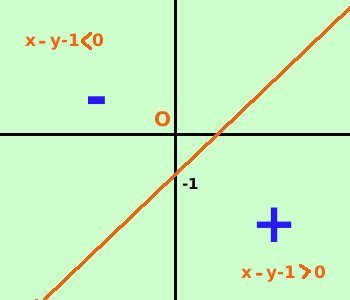
essa nel piano cartesiano rappresenta una retta che divide il piano in due parti In una delle due parti allora l'espressione x - y - 1 sara' positiva, mentre nell'altra parte sara' negativa Per decidere in quale delle due parti e' positiva basta sostituire ad x e ad y un valore di qualunque punto che si trovi in una delle due parti; ad esempio considero il punto origine O e sostituisco zero ad x e ad y; ottengo: 0 + 0 - 1 < 0 quindi nella parte dove e' l'origine l'espressione e' negativa mentre nell'altra parte l'espressione e' positiva L'espressione nulla e' rappresentata dai punti della retta La soluzione alla nostra disequazione e' quindi rappresentata dal semipiano che si trova sotto la retta (retta compresa) |

|

|

|

|