Segno di espressioni prodotto di due o piu' espressioni elementari Vediamo di ragionare su un esempio pratico Consideriamo un'espressione del tipo x2 - 6x + 8 > 0 Voglio trovare l'insieme dei valori che posso assegnare alla x perche' l'espressione sia maggiore di zero Considero l'equazione associata x2 - 6x + 8 = 0 Risolvo          6 (62 - 4·1·8) x1,2 = ----------------------       calcoli                   2 x1 = 2 x2 = 4 allora posso sostituire la disequazione di partenza con l'espressione equivalente (x-2)(x-4)>0 Essendo questa espressione prodotto di due termini sara' maggiore di zero quando i due termini che la compongono hanno lo stesso segno, cioe' entrambe maggiori di zero oppure entrambi minori di zero. Quindi dovrei risolvere i due sistemi: x - 2 > 0 x - 4 > 0 x - 2 < 0 x - 4 < 0 Capisci che questo sarebbe un metodo molto pesante, soprattutto se invece del prodotto di due termini l'espressione fosse il prodotto di 3,4,5... termini. Allora mettiamo in un grafico il segno di ognuno dei termini e poi scegliamo gli intervalli dove i segni sono concordi (entrambe positivi od entrambe negativi) Poniamo sempre tutti i fattori componenti maggiori di zero per trovare i segni, indicando poi su un grafico dove sono positivi e dove negativi; poi se dovremo risolvere una disequazione positiva prenderemo gli intervalli dove il prodotto e' positivo; se dobbiamo cercare dove la disequazione e' negativa prenderemo gli intervalli dove il prodotto dei fattori diventa negativo Risolvo la prima disequazione x - 2 > 0          x > 2   il primo fattore e' positivo per x maggiore di due Risolvo la seconda x - 4 > 0          x > 4   il secondo fattore e' positivo per x maggiore di quattro faccio lo schema        Hai bisogno di aiuto per fare lo schema? x > 2                    - - - - - (2) + + + + + + + + + + + + + + + x > 4                     - - - - - - - - - - - - (4) + + + + + + + + + Espressione          + + + + (2) - - - - - (4) + + + + + + + + + L'espressione e' positiva dove i due fattori sono entrambe positivi ed anche dove sono entrambe negativi, quindi avremo x < 2 V x > 4 oppure in altra notazione 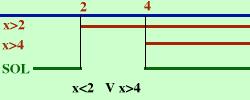in tal caso si intende positivo dove si indica con la linea intera e negativo ove la linea manca (oppure qualche professore preferisce farla tratteggiata). Invece di SOL (soluzione) di solito si preferisce mettere f(x) Ricapitolando: Se devi risolvere una disequazione di grado superiore Devi considerare l'equazione associata e risolverla per trovare le soluzioni Devi poi scomporre la disequazione in prodotto di fattori di primo grado Poni tutte i fattori di primo grado maggiori di zero Costruisci un grafico dove metti tutti i valori positivi e negativi trovati In fondo al grafico fai il calcolo dei segni del prodotto fra i singoli fattori Se la disequazione e' maggiore di zero consideri come soluzione i valori in cui il prodotto dei fattori e' positivo Se la disequazione e' minore di zero consideri come soluzione i valori in cui il prodotto dei fattori e' negativo Piu' avanti, quando avremo visto le regole per risolvere le disequazioni di secondo grado scomporremo le disequazioni di grado superiore come prodotto di fattori composti da equazioni (polinomi) sia di primo che di secondo grado Approfondimento per disequazioni con o con e con un termine di grado superiore ad 1: Se abbiamo disequazioni dove dobbiamo studiare anche il caso di uguaglianza a zero e' necessario distinguere fra l'equazione e la disequazione e risolvere sia l'equazione che la disequazione e quindi considerare entrambe i risultati: Normalmente, se abbiamo tutti fattori di primo grado, si procede senza farci troppo caso, in questo modo risolvo gli esercizi 2,3 e 4 Invece, nell'esercizio 5, la presenza del fattore x2 puo' generare errore ed e' effettivamente necessario dividere l'equazione e la disequazione Vediamo alcuni esercizi x2 - x - 6 < 0           Soluzione x2 + 2x - 3 0            Soluzione x2 - 3x - 10 0        Soluzione x4 - 5x2 + 4 0        Soluzione x2(x-1) 0            Soluzione