Disequazioni con moduli La trattazione del modulo e' sempre la stessa sia che si tratti di equazioni di primo grado, che di disequazioni. In pratica devi suddividere la retta reale in parti e in ogni parte devi considerare la disequazione (l'equazione) tale che la parte interna del modulo sia maggiore di zero. Accetterai pero' solo le soluzioni che cadono entro gli intervalli in cui sono valide le disequazioni (le equazioni) vediamo un esempio 2x + |x-3| 0 Il modulo |x-3| e' sempre definito positivo, quindi dov'e' positivo lo prendo com'e', dov'e' negativo lo cambio di segno |x-3| = x-3 se x 3 |x-3| = -x+3 se x 3 Nota: quando risolvi il modulo devi mettere una delle parti anche uguale a zero oltre che maggiore o minore, e' indifferente se mettere l'uguale assieme col maggiore od assieme col minore, l'importante e' metterlo (io, in questa pagina lo mettero' assieme col minore) Quindi divido la retta reale nei due intervalli da meno infinito a 3 compreso ove la disequazione diventa 2x - x + 3 0 da 3 a piu' infinito ove la disequazione diventa 2x + x - 3 0 Cioe' devo risolvere i due sistemi x 3 2x - x + 3 0 e x 3 2x + x - 3 0 Risolvo il primo x 3 2x - x + 3 0 x 3 x -3 facendo lo schema    se hai bisogno di aiuto per lo schema 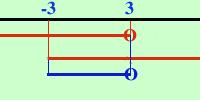ottengo -3 x 3 Risolvo il secondo x 3 2x + x - 3 0 x 3 x 1 facendo lo schema    se hai bisogno di aiuto per lo schema 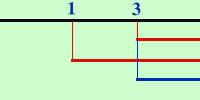ottengo x 3 Ora metto assieme le soluzioni dei due sistemi ed ottengo x -3