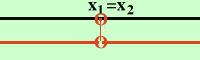
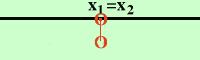
Parabola tangente all'asse delle x E' equivalente al caso ove il delta del polinomio e' uguale a zero (2 soluzioni reali coincidenti = 2 punti coincidenti, cioe' un solo punto sull'asse x) Distinguiamo i due casi: 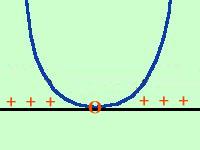a 0 a 0 a 0 Se a e' maggiore di zero la parabola ha la concavita' verso l'alto quindi avremo che il trinomio e' positivo per tutti i valori eccetto il valore del vertice -b/2a per cui si annulla 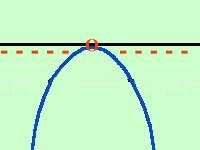=0 a 0 ax 2 + bx + c 0 ax2 + bx + c 0 tutti i valori eccetto -b/2a per cui si annulla nessun valore a 0 Se a e' minore di zero la parabola ha la concavita' verso il basso quindi avremo che il trinomio e' negativo per tutti i valori eccetto il valore del vertice -b/2a per cui si annulla =0 a 0 ax 2 + bx + c 0 ax2 + bx + c 0 nessun valore tutti i valori eccetto -b/2a per cui si annulla