Esercizio su disequazione di quarto grado risolviamo la disequazione: x4 - 16 ---------------------- x4 + x3 - x - 1    0 Scomponiamo in fattori sia il numeratore che il denominatore Scomposizione del numeratore Considero il polinomio associato x4 - 16 = devo scomporlo in fattori; sono 2 termini,e' una differenza di quadrati x4 - 16 = (x2 - 4)(x2 + 4) = il primo fattore e' ancora una differenza di quadrati mentre il secondo come somma di quadrati non e' piu' scomponibile = ( x - 2)(x + 2)(x2 + 4) Scomponiamo il denominatore Considero il polinomio associato x4 + x3 - x - 1 = sono 4 termini: Non e' il cubo di un binomio Puo' essere un raccoglimento parziale provo a scomporre come raccoglimento parziale x4 + x3 - x - 1 = x3(x+1) - 1(x+1) = (x+1)(x3 - 1) = L'ultimo fattore (2 termini) come differenza di cubi e' scomponibile, quindi ottengo = (x+1)(x-1)(x2+x+1) L'ultimo fattore non e' piu' scomponibile quindi ottengo ( x - 2)(x + 2)(x2 + 4) ------------------------------ (x+1)(x-1)(x2+x+1)    0 Poniamo ogni fattore del numeratore maggiore od uguale a 0 ed ogni fattore del denominatore solamente maggiore di zero (lo zero non puo' mai essere al denominatore) x - 2 0       x 2 x + 2 0      x -2 x2 + 4 0       sempre vero (delta minore di zero) x + 1 > 0       x > -1 x - 1 > 0       x > 1 x2+x+1 > 0       sempre vero (delta minore di zero) 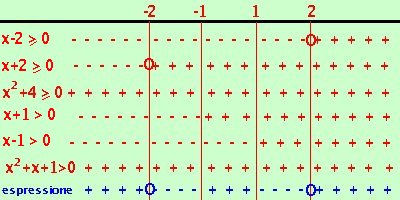Adesso riporto i risultati su un grafico indicando con un un + dove ogni disequazione e' verificata e con un - dove non e' verificata inoltre indico con un cerchietto i punti dove il fattore vale zero ed e' accettabile e poi faccio il conto dei segni: devo prendere gli intervalli dove il prodotto dei segni dei fattori (cioe' il segno dell'espressione) risulta positivo o nullo. Ottengo come risultato: x -2   U   -1 < x < 1   U   x 2 Nota che anche qui avrei potuto tralasciare i due fattori con delta minore di zero perche',essendo positivi, non influiscono sul segno del risultato