Problema Calcolare il perimetro di un rettangolo sapendo che la base e' tripla dell'altezza e che, se si diminuiscono entrambe di 1 metro la superficie del rettangolo diminuisce di 15 m2 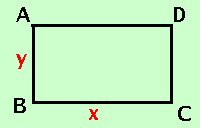Come prima cosa costruiamo la figura La prima relazione dice che la base e' tripla dell'altezza BC _ =  3 AB _ La seconda relazione dice che diminuendo di 1 sia la base che l'altezza l'area diminuisce di 15 m2 Sviluppo (  BC _-  1) · (  AB _-  1) =  BC _· AB _-  15m2 Per calcolare il perimetro devo trovare la misura dei lati, quindi pongo BC _ = x         AB _ = y sostituisco nella prima relazione x = 3y sostituisco nella seconda relazione (x-1)(y-1) = xy - 15   Calcoli x + y = 16 Metto a sistema le due relazioni x = 3y x + y = 16 sostituisco il valore della x della prima equazione nella seconda equazione x = 3y 3y + y = 16 sommo x = 3y 4y = 16 nella seconda equazione divido entrambe i termini per 4 x = 3y y = 4 Sostituisco il valore della y che ho trovato, nella prima equazione x = 3·4 y = 4 x = 12 y = 4 Quindi: BC _ = x = 12 m       AB _ = 4 m Devo trovare il perimetro (AB=CD e BC=AD) AB _ +  BC _ +  CD _ +  AD _ = 4m + 12m + 4m + 12 m = 32m