Calcoli Calcoliamo il valore del determinante           1    1     6  1    1     5  1   -1     2 Applichiamo la regola di Sarrus riportando la prima e la seconda colonna   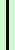        1    1     6  1    1     5  1   -1     2  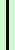1    1  1    1  1   -1 Moltiplico prima gli elementi della diagonale principale e delle due diagonali parallele   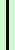        1    1     6  1    1     5  1   -1     2  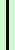1    1  1    1  1   -1 = 1·1·2 + 1·5·1 + 6·1·(-1) = 2 + 5 - 6 = 1 Moltiplico poi gli elementi della diagonale secondaria e delle due diagonali parallele   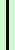        1    1     6  1    1     5  1   -1     2  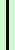1    1  1    1  1   -1 = 6·1·1 + 1·5·(-1) + 1·1·2 = 6 - 5 + 2 = 3 Adesso faccio la differenza fra i due valori trovati ed ottengo il valore del determinante  1    1     6  1    1     5  1   -1     2 = 1 - 3 = -2