Disequazione elementare del tipo
F(x) <  G(x) G(x)
Dobbiamo risolvere:
F(x) <  G(x) G(x)
Intanto abbiamo due possibilita':
a) se F(x) > 0 allora
- Il termine sotto radice (radicando) deve sempre essere maggiore di zero
G(x) > 0
- per ipotesi
F(x) > 0
- Il quadrato del primo termine dovra' essere minore del quadrato del secondo termine
[ F(x)]2 < G(x)
La prima condizione e' gia' contenuta nella terza (G(x) e' maggiore di un quadrato che e' certamente positivo) quindi
l'espressione si trasforma nel sistema
 F(x) > 0
F(x) > 0
[ F(x)]2 < G(x)
b) se F(x) < 0 allora
perche' la disequazione sia verificata e' sufficiente che il termine sotto radice (radicando) sia maggiore o uguale a zero G(x)  0, perche' in tal caso posso fare il radicale ed il radicale e' definito positivo o nullo
quindi
l'espressione si trasforma nel sistema 0, perche' in tal caso posso fare il radicale ed il radicale e' definito positivo o nullo
quindi
l'espressione si trasforma nel sistema
 F(x) < 0
F(x) < 0
G(x)  0 0
Raccogliendo devo risolvere i due sistemi:
 |
F(x)  0 0
[ F(x)]2 < G(x)
|
|
 |
F(x) < 0
G(x)  0 0
|
Nella prima poniamo anche F(x) = 0 per cercare tutte le soluzioni
E la soluzione dei sistemi fornira' le soluzioni della disequazione
se abbiamo F(x)  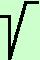 G(x)
allora otterremo G(x)
allora otterremo
 |
F(x)  0 0
[ F(x)]2  G(x) G(x)
|
|
 |
F(x) < 0
G(x)  0 0
|
Vediamo ora un paio di esercizi:
|



