|
Se considero una funzione e la sua derivata prima abbiamo gia' visto la relazione 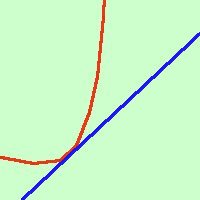 (y - y0) =
f '(x0)·( x -
x0)
(y - y0) =
f '(x0)·( x -
x0)
o meglio y = f '(x0)·( x - x0)+ y0 Questo significa che con la derivata prima posso approssimare la curva in un punto con una retta (la tangente) Intuitivamente possiamo dire che la curva e la tangente hanno due punti (coincidenti) comuni 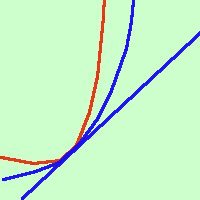 se consideriamo oltre la derivata prima anche la derivata seconda otterremo una curva del secondo ordine (parabola) che ha tre punti comuni con la curva in esame (parabola osculatrice) e quindi otterremo un'approssimazione migliore 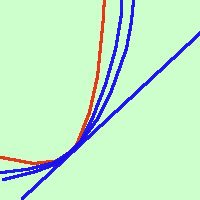 Se consideriamo poi anche la derivata terza otterremo una curva del terzo ordine con quattro punti in comune con la curva in esame (cubica osculatrice) e quindi l'approssimazione migliorera'
Se consideriamo poi anche la derivata terza otterremo una curva del terzo ordine con quattro punti in comune con la curva in esame (cubica osculatrice) e quindi l'approssimazione migliorera'Quindi piu' derivate successive prendero' meglio approssimero' la curva, e posso procedere fino ad approssimare la curva quanto voglio. peccato che il metodo serva solo a livello locale, cioe' in un intorno abbastanza ristretto del punto considerato, ma vedremo che dara' luogo a parecchie conclusioni interessanti |

|

|

|

|