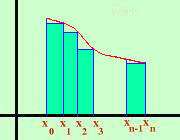
 Faccio la somma delle varie aree dei rettangoli interni Indico l'altezza di ogni rettangolo con f(xk); per ora questo valore e' il valore minimo della funzione nell'intervallo considerato; in seguito vedremo che puo' essere un qualunque valore della funzione nell'intervallo le basi saranno i segmenti: (x1 - x0) (x2 - x1) (x3 - x2) (x4 - x3) ...... (xk - xk-1) ...... (xn - xn-1) Le aree quindi saranno:
 f(xk)·(xk -
xk-1)
f(xk)·(xk -
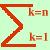
xk-1)Nota:  Abbiamo fatto l'esempio con una funzione decrescente, potevamo farlo con una funzione crescente, in tal caso, per calcolare le aree avremmo dovuto prendere come altezza le funzioni calcolate all'inizio degli intervalli
Abbiamo fatto l'esempio con una funzione decrescente, potevamo farlo con una funzione crescente, in tal caso, per calcolare le aree avremmo dovuto prendere come altezza le funzioni calcolate all'inizio degli intervalli
Area primo rettangolo (x1 - x0)·f(x0), Area secondo rettangolo (x2 - x1)·f(x1), Area terzo rettangolo (x3 - x2)·f(x3), Area quarto rettangolo (x4 - x3)·f(x3), ........ Area (n-1)-esimo rettangolo (xn-1 - xn-2)·f(xn-2), Area n-esimo rettangolo (xn - xn-1)·f(xn-1), 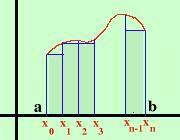
pero' si puo' dimostrare che, al diminuire dell'intervallo, non ha piu' importanza considerare un estremo piuttosto che l'altro, perche' quando l'intervallo e' molto piccolo i valori agli estremi dell'intervallo considerato tenderanno a diventare uguali e quindi e' possibile applicare il ragionamento anche a funzioni non monotone considerando, per essere precisi, il punto di minimo nell'intervallo e d'ora in avanti faremo cosi' |

|

|

|

|