|
L'asse di un segmento, definito in geometria come la perpendicolare condotta al segmento nel suo punto di mezzo puo' essere definito anche come luogo geometrico: 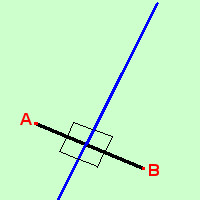 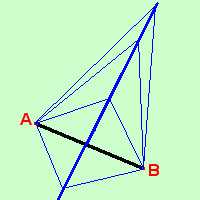 L'asse di un segmento e' il luogo geometrico dei punti del piano che hanno la stessa distanza dagli estremi del segmento Da notare che posso definire lo stesso luogo geometrico in vari modi: ad esempio potrei definire l'asse del segmento anche come il luogo dei vertici dei triangoli isosceli aventi come base il segmento stesso ed altezza variabile Per ricavare l'equazione dell'asse di un segmento conoscendone gli estremi potremmo calcolarne il punto medio, calcolare l'equazione della retta passante per gli estremi del segmento (retta su cui giace il segmento) quindi calcolare la perpendicolare condotta a tale retta nel punto medio trovato Qui invece troviamone l'equazione come luogo geometrico: consideriamo un segmento di estremi A(x1;y1) e B(x2;y2) con x1;y1;x2;y2 valori noti Consideriamo poi un punto generico P(x;y) Imponiamo la condizione che la distanza PA sia uguale alla distanza PB PA = PB √ [(x-x1)2 + (y-y1)2] = √ [(x-x2)2 + (y-y2)2] Elevo al quadrato entrambe i membri cosi' spariscono le radici (x-x1)2 + (y-y1)2 = (x-x2)2 + (y-y2)2 x2-2xx1 + x12 + y2-2yy1 + y12 = x2-2xx2 + x22 + y2-2yy2 + y22 Elimino i termini uguali da parti opposte dell'uguale -2xx1 + x12 -2yy1 + y12 = -2xx2 + x22 -2yy2 + y22 porto tutto prima dell'uguale -2xx1 + x12 -2yy1 + y12 +2xx2 - x22 +2yy2 - y22 = 0 ora raccolgo tra loro i termini con la x, i termini con la y ed infine i termini noti x(-2x1+2x2) + y(-2y1 + 2y2) + (x12 + y12 + x22 + y22) La rendo un poco piu' "elegante" ed ottengo la formula finale
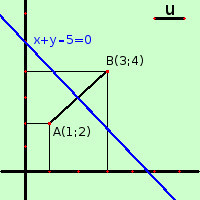Esempiotrovare l'asse del segmento di estremi A(1;2) B(3;4) Ho x1=1 y1=2 x2=3 y2=4 applico la formula 2x(3-1) + 2y(4-2) + (12 + 22 - 32 - 42) = 0 2x(2) + 2y(2) + (1 + 4 - 9 - 16) = 0 4x + 4y - 20 = 0 semplifico per 4 x + y - 5 = 0 in forma esplicita y = -x +5 |
|
|
|
|