 
La bisettrice di un angolo, definita in geometria come la retta che divide l'angolo a meta' puo' essere definita anche come luogo geometrico:
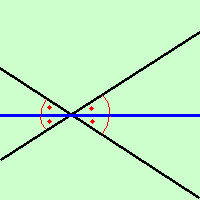
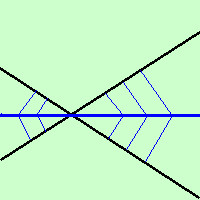
La bisettrice di un angolo e' il luogo geometrico dei punti del piano che hanno la stessa distanza dai lati dell'angolo stesso Da notare che posso definire lo stesso luogo geometrico in vari modi: ad esempio potrei definire la bisettrice dell'angolo anche come il luogo dei punti medi delle basi dei triangoli isosceli aventi come vertice l'angolo stesso Troviamone l'equazione come luogo geometrico: consideriamo due rette r1) ax + by +c = 0 e r2) dx + fy +e = 0 con a, b, c, d, e, f valori noti e consideriamo un punto generico P(x;y) del piano Imponiamo la condizione che la distanza fra P ed r1 sia uguale alla distanza fra P ed r2
la prendiamo come formula finale: comunque si vede che si tratta dell'equazione di una retta essendo le x e le y a potenza 1; anzi le rette sono 2; una ha i denominatori positivi oppure negativi (basta cambiare tutto di segno per vedere che sono la stessa retta), l'altra i denominatori uno positivo e l'altro negativo (o viceversa) e sono tra loro perpendicolari Esempio trovare la bisettrice dell'angolo formato dalle rette r1) 3x + 4y + 12 = 0 r2) √3 x - y + 2√3 = 0 Le bisettrici sono 2, tra loro perpendicolari; Per semplificare un po' troviamo la bisettrice che ha lo stesso segno ad entrambe i termini al denominatore, un analogo sviluppo con i denominatore uno positivo e l'altro negativo portera' all'altra bisettrice (nel grafico te la tratteggio in nero) Siccome cambiando entrambe i segni al denominatore l'uguaglianza non cambia consideriamo entrambe i denominatori positivi Ho a = 3 b = 4 c = 12 d = √3 e = -1 f = 2√3 applico la formula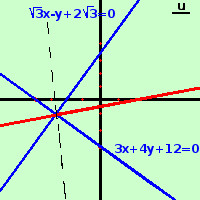 
6x+8y+24 = 5x√3 -5y + 10√3 essendo 6 minore di 5√3 porto tutto dopo l'uguale 0 = x(5√3-6) +(-5-8)y + 10√3-24 leggo alla rovescia e sommo dove possibile x(5√3-6) - 13y + 10√3-24 = 0 Questa e' l'equazione della bisettrice a destra il grafico fare il grafico |
|
|
|
|