Studio della parabola
y = -x2 - 3x + 4
Si tratta di una parabola del tipo y=ax2 +bx +c con asse verticale
- troviamo l' intersezione con l'asse y
- troviamo le intersezioni con l'asse x
- troviamo l'equazione dell'asse verticale
- troviamo le coordinate del vertice
- riportiamo i risultati su un piano cartesiano
- troviamo l' intersezione con l'asse y
Dobbiamo fare il sistema fra la parabola e l'asse delle y (x=0); per fare prima basta porre nell'equazione x=0, troviamo
y = -02 - 3·0 + 4 = 4
Quindi avremo il punto di intersezione di coordinate C≡(0;4)
- troviamo le intersezioni con l'asse x
Dobbiamo fare il sistema fra la parabola e l'asse delle x (y=0); per fare prima basta porre nell'equazione y=0, e troviamo
y = -x2 - 3x + 4
0 = -x2 - 3x + 4
x2 +3x -4 = 0
otteniamo
x1 = -4 x2 = 1
calcoli
Quindi avremo i punti di intersezione di coordinate A≡(-4;0) e B≡(1;0)
- troviamo l'equazione dell'asse verticale
L'asse verticale ha la formula x=-b/2a con b=-3 ed a=-1,
quindi l'asse verticale ha equazione x=-3/2
- troviamo le coordinate del vertice
Le coordinate del vertice sono
| V≡(
|
-b

2a
|
;
|
b2 - 4ac
- 
4a
|
)
|
Abbiamo a=-1, b=-3 e c=4 sostituendo abbiamo
| V≡(
|
-(-3)

2·(-1)
|
;
|
(-3)2 - 4·(-1)·4
- 
4·(-1)
|
)
|
| V≡(
|
3

-2
|
;
|
9 + 16
- 
-4
|
)
|
V≡(-3/2; 25/4)
- riportiamo i risultati su un piano cartesiano
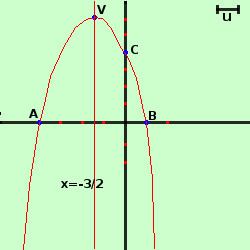
|