Poligoni regolari Apriamo una parentesi per approfondire il concetto di poligono regolare Definizione: un poligono e' regolare se ha tutti i lati congruenti e tutti gli angoli congruenti Avremo quindi: Triangolo equilatero: e' un triangolo con i tre lati congruenti ed i tre angoli congruenti (quindi, essendo 180° la somma degli angoli interni, ha tre angoli di 60°) Quadrato: e' un quadrilatero con i quattro lati congruenti ed i quattro angoli congruenti (quindi, essendo somma angoli interni = 2 angolipiatti = 360° la somma degli angoli interni, ha quattro angoli di 90°) 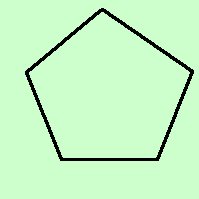Pentagono regolare: e' un poligono con i cinque lati congruenti ed i cinque angoli congruenti (quindi, essendo somma angoli interni = 3 angolipiatti = 540° il poligono ha cinque angoli interni di 108°) 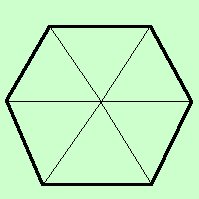Esagono regolare: e' un poligono con i sei lati congruenti ed i sei angoli congruenti (quindi, essendo somma angoli interni = 4 angolipiatti = 720° il poligono ha sei angoli interni di 120°) Considerando il centro del cerchio circoscritto posso suddividerlo in 6 triangoli equilateri E cosi' via di seguito hai: ettagono regolare (con 7 lati) ottagono regolare (con 8 lati) ennagono regolare (con 9 lati) decagono regolare (con 10 lati) undecagono regolare (con 11 lati) dodecagono regolare (con 12 lati) poligono regolare con 13 lati poligono regolare con 14 lati eccetera ............ Vale la proprieta': Tutti i poligoni regolari sono sia inscrittibili che circoscrittibili ad una circonferenza Considerando il centro della circonferenza circoscritta (od inscritta) e tracciando le congiungenti i vertici del poligono ogni poligono viene suddiviso in triangoli congruenti. L'altezza di ognuno di questi triangoli ha un nome speciale: Apotema