|
Vediamo ora quali sono le possibili posizioni di due circonferenze caratterizzandole con la distanza fra i centri ed i raggi Per capire bene procurati due monete di diametro diverso, ad esempio una moneta da 10 centesimi ed una da 50 e prova a vedere, avicinandole, quante posizioni diverse si possono avere Abbiamo sei possibilita' 1 circonferenze esterne 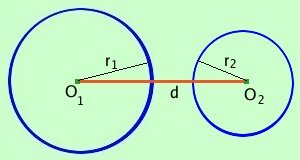
O1 O2____ > r1 + r2 d > r1+ r2 Le circonferenze sono fra loro esterne se la distanza d fra i due centri e' superiore al valore della somma dei due raggi Viceversa: se la distanza fra i due centri e' superiore al valore della somma dei due raggi allora le circonferenze sono esterne fra loro 2 circonferenze tangenti esternamente 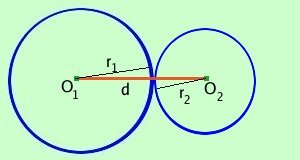
O1 O2____ = r1 + r2 d = r1+ r2 Le circonferenze sono fra loro tangenti esternamente se la distanza d fra i due centri e' uguale al valore della somma dei due raggi Viceversa: se la distanza fra i due centri e' uguale al valore della somma dei due raggi allora le circonferenze sono tangenti esternamente fra loro 3 circonferenze secanti 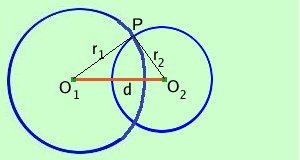
r1 + r2 > O1 O2____ > r1 - r2 d < r1+ r2 Le circonferenze sono fra loro secanti se la distanza d fra i due centri e' inferiore al valore della somma dei due raggi e superiore alla loro differenza Viceversa: se la distanza fra i due centri e' inferiore al valore della somma dei due raggi e superiore alla loro differenza allora le circonferenze sono fra loro secanti Deriva dalla proprieta' dei triangoli per cui un lato O1O2 e' minore della somma degli altri due lati PO1 +PO2 ed e' anche maggiore della loro differenza PO1-PO2 4 circonferenze tangenti internamente 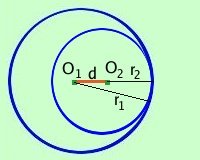
O1 O2____ = r1 - r2 d = r1 - r2 Le circonferenze sono fra loro tangenti internamente se la distanza d fra i due centri e' uguale al valore della differenza dei due raggi Viceversa: se la distanza fra i due centri e' uguale al valore della differenza dei due raggi allora le circonferenze sono fra loro tangenti esternamente 5 circonferenza interna 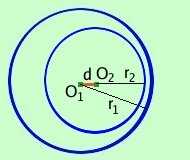
r1 - r2 > O1 O2____ > 0 r1 - r2 > d > 0 Una circonferenza e' interna rispetto all'altra se la distanza d fra i due centri e' inferiore al valore della differenza dei due raggi ma e' maggiore di zero Viceversa: se la distanza fra i due centri e' inferiore al valore della differenza dei due raggi ed e' magiore di zero allora una circonferenza e' interna rispetto all'altra 6 circonferenze concentriche 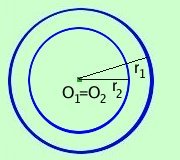
O1 O2____ = 0 d = 0 Le circonferenze sono concentriche se la distanza d fra i due centri e' uguale a zero Viceversa: se la distanza d fra i due centri e' uguale a zero allora le circonferenze sono concentriche |

|

|

|

|