Proprieta' della bisettrice dell'angolo esterno di un triangolo Intanto dobbiamo dire che il teorema e' valido solamente se la bisettrice dell'angolo esterno incontra il prolungamento del lato del triangolo opposto al vertice da cui si traccia la bisettrice; essendo valida questa condizione possiamo procedere C'e' anche da dire che questo e' un teorema minore e, francamente, non ho mai avuto occasione di applicarlo in nessun problema, quindi se vuoi trascurarlo va bene, basta che ti ricordi che esiste Vale il teorema: Se la bisettrice dell'angolo esterno di un triangolo incontra il prolungamento del lato opposto al vertice considerato, allora i segmenti congiungenti il punto di incontro con i vertici del lato opposto sono proporzionali agli altri due lati So che la retta AD e' la bisettrice dell'angolo esterno CAF; devo dimostrare che vale BD : CD = BA : AC Ipotesi      CAD = DAF ^ ^             Tesi BD : CD = BA : AC Dimostrazione: Intuitivamente: anche qui dobbiamo far vedere che vale il teorema di Talete, quindi cercheremo, mediante costruzioni, di richiamare la figura del teorema di Talete 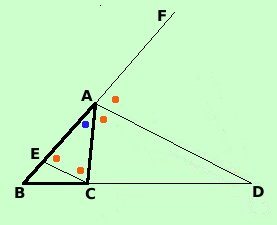Prolungo il segmento BC dalla parte di C fino ad incontrare la bisettrice nel punto D Dal punto C mando la parallela alla retta DA che incontra il lato AB nel punto E abbiamo che CAD = ACE ^ ^ perche' alterni interni rispetto alle parallele AD ed EC tagliate dalla trasversale AC FAD = AEC ^ ^ perche' corrispondenti rispetto alle parallele AD ed EC tagliate dalla trasversale AE di conseguenza AEC = ACE ^ ^perche' congruenti ad angoli congruenti per ipotesi ed il triangolo AEC e' isoscele, di conseguenza avremo EA = AC Per il teorema di Talete applicato alle parallele EC ed AD tagliate dalle trasversali BF e BD possiamo scrivere BC : CD = BE : EA applico la proprieta' del comporre (BC+CD) : CD = (BE+EA) : EA sommo BD : CD = BA : EA siccome EA =AC sostituendo nella proporzione otteniamo la tesi BD : CD = BA : AC come volevamo