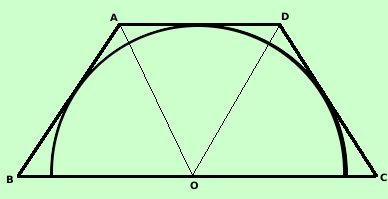
Trapezio isoscele circoscritto ad una semicirconferenza con lato obliquo congruente alla base minore Veramente nei libri di testo questo esempio non l'ho mai visto, pero' siccome ho trovato nella mia carriera tanti problemi che si basavano su di esso, penso che meriti di essere considerato fra gli altri casi Considero un trapezio isoscele circoscritto ad una semicirconferenza in cui il lato obliquo sia congruente alla base minore: 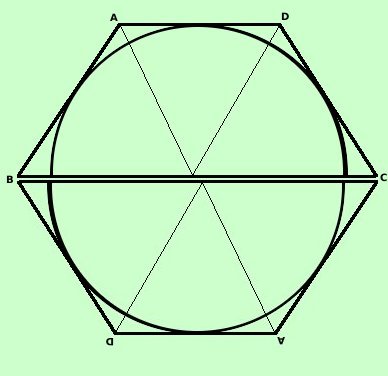La figura corrisponde a meta' dell'esagono regolare circoscritto all'intera circonferenza: e pertanto potremo basarci su di essa per discuterla: infatti se considero il trapezio isoscele circoscritto ad una semicirconferenza con lato obliquo congruente alla base minore e lo "ribalto" attorno alla base maggiore ottengo un esagono regolare quasi regolare: colpa mia! 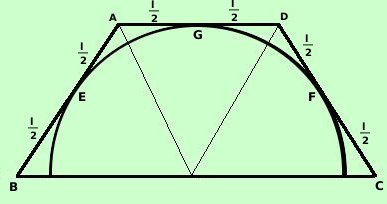Non sono troppo preciso nel disegno Una proprieta' abbastanza interessante e' data dal fatto che i segmenti di tangente condotti da un puunto esterno ad una circonferenza sono fra loro congruenti, quindi, avremo che i lati obliqui e la base minore del trapezio sono suddivisi a meta' dal punto di tangenza al cerchio: BE = EA = AG = GD = DF = FC = l/2 In genere posso considerare tre tipi di problemi: Dato il valore del lato obliquo risolvere il trapezio 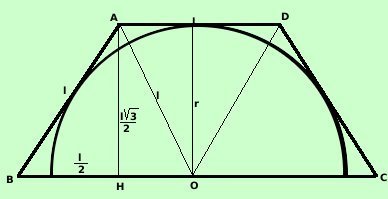Supponiamo di conoscere il valore l del lato obliquo AB = CD = AD = l inoltre: BC = BO + OC = l + l =2 l Se considero il semicerchio inscritto, congiungendo i vertici con il centro del semicerchio posso dividere il trapezio in tre triangoli equilateri: consideriamo il triangolo equilatero ABO L'altezza AH lo divide in due triangoli rettangoli con angoli di 30° e 60°: considero il triangolo ABH Posso trovare il valore di AH altezza del trapezio AH = l3 --------- 2 = raggio del cerchio circoscritto Inoltre, essendo i triengoli equilateri, conosco anche il valore della base maggiore BC = 2l Problemi collegati al gran numero di triangoli rettangoli che si possono formare nella figura: 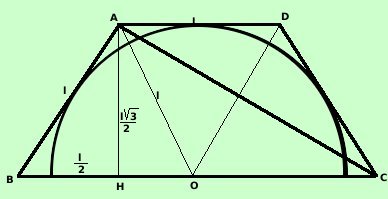Congiunto un vertice della base maggiore con il vertice opposto della base minore risolvere il triangolo rettangolo che cosi' si viene a formare: Il triangolo (ad esempio ABC)che si forma ha un lato doppio dell'altro ed un angolo di 60° come anche il triangolo ABH Quindi i due triangoli ABC ed ABH sono simili per il secondo criterio di similitudine quindi anche ABC e' un triangolo rettangolo con angoli di 30° e 60° Naturalmente sono rettangoli anche i triangoli in cui ABC e' diviso dalla sua altezza relativa all'ipotenusa Se inoltre considero il quadrilatero AOCD esso e' un rombo e viene diviso dalle sue diagonali in 4 triangoli rettangoli anche questi con angoli di 30° e 60° Pensa che oltre cio' e' possibile considerare anche la congiungente BD e quindi.... 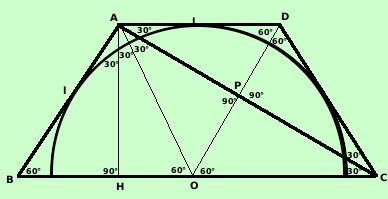Problemi collegati al valore degli angoli ti illustro nella figura i valori di alcuni angoli: da questi puoi renderti conti di quali e quanti problemi si potrebbero costruire con questa figura