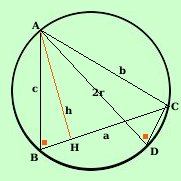
Relazione fra raggio del cerchio e lati del triangolo inscritto Teorema: Il raggio del cerchio in cui e' inscritto un triangolo e' uguale al prodotto dei lati fratto 4 volte l'area del triangolo stesso. cioe' chiamate a, b e c le misure dei lati del triangolo e chiamata As la sua area vale la relazione: r = a b c ----------- 4As Poniamo BC = a___ AC = b___ AB = c___ Dimostrazione Considero l'altezza del triangolo ABC sul lato BC e la chiamo h AH = h___ Ora dal punto A traccio il diametro AD della circonferenza AD = 2r___ Congiungendo D con C ottengo il triangolo ADC Considero ora i triangoli ABH ed ADC essi hanno: AHB = ACD^^ perche' retti ABC = ADC^^ perche' angoli alla circonferenza che insistono sullo stesso arco AC: quindi i due triangoli sono simili per il primo criterio di similitudine e posso scrivere: AB : AD = AH : AC utilizzando le misure c : 2r = h : b 2rh = bc moltiplico entrambe i membri per a 2arh = abc Ma ah/2 e' l'area As del triangolo quindi 2ah e' 4 volte l'area 4As r·4As = abc ricavo r r = abc ---------- 4 As come volevamo