Volume del parallelepipedo rettangolo Procediamo ora a calcolare il primo volume: per questo abbiamo bisogno del teorema: Due parallelepipedi rettangoli aventi le basi congruenti hanno i volumi proporzionali alle rispettive altezze               Se hai bisogno della dimostrazione 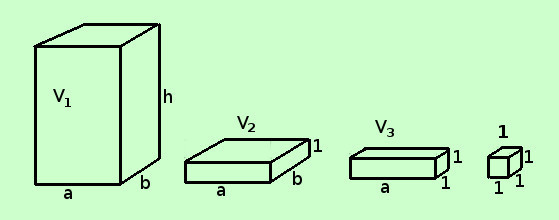Dimostriamo il teorema: Il volume del parallelepipedo rettangolo si misura con il prodotto delle sue tre dimensioni V = a·b·h Consideriamo il parallelepipedo rettangolo di dimensioni a, b e h di volume V1 ed anche il parallelepipedo rettangolo di dimensioni a, b e 1 di volume V2; per il teorema di inizio pagina posso scrivere V1 V2 = h 1 Consideriamo poi il parallelepipedo rettangolo di dimensioni a, b e 1 di volume V2 ed anche il parallelepipedo rettangolo di dimensioni a, 1 e 1 di volume V3; per il teorema di inizio pagina posso scrivere V2 V3 = b 1 Consideriamo infine il parallelepipedo rettangolo di dimensioni a, 1 e 1 di volume V3 ed anche il parallelepipedo rettangolo di dimensioni 1, 1 e 1 di volume 1 (unita' di misura); per il teorema di inizio pagina posso scrivere V3 1 = a 1 Adesso prendiamo le tre uguaglianze e moltiplichiamo fra loro i termini prima dell'uguale e tra loro i termini dopo l'uguale V1 V2 · V2 V3 · V3 1 = h 1 · b 1 · a 1 e, semplificando numeratore e denominatore otteniamo V1 = a·b·h e, generalizzando, per un generico volume V Parallelepipedo rettangolo Volume = a·b·h Come volevamo Siccome l'area del rettangolo di base si trova facendo Asb = a·b avremo la formula Parallelepipedo rettangolo Volume = Asb·h Il volume del parallelepipedo rettangolo si trova moltiplicando l'area di base per la misura dell'altezza Infine vediamo il volume del cubo che possiamo considerare come un parallelepipedo rettangolo con le tre dimensioni uguali l = a = b = c Cubo Volume = l·l·l = l3 Il volume del cubo si trova elevando alla terza la misura di un suo lato