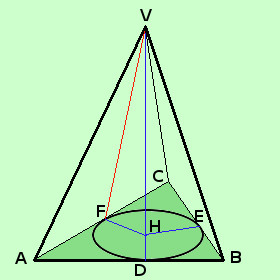
 Per poter avere esercizi abbastanza semplici, senza dover fare un calcolo per ogni faccia della piramide abbiamo bisogno di pensare a piramidi che abbiano le facce uguali, od almeno con le stesse altezze; diventa quindi essenziale pensare piramidi che abbiano delle particolari caratteristiche Intendiamoci: nulla vieta di fare esercizi con piramidi oblique e mi ricordo che in un tema d'esame della maturita' magistrale si dovevano calcolare tutti gli spigoli e le altezze delle varie facce diverse fa loro, ma nella mia carriera gli esercizi che ho visto di questo tipo si contano sulle dita di una mano Consideriamo l'insieme dei poligoni circoscritti ad una circonferenza: se la nostra piramide ha come base uno di tali poligoni e la perpendicolare dal vertice cade esattamente nel centro del cerchio inscritto nel poligono allora diremo che tale piramide e' retta Ceme esempio in figura hai una piramide triangolare retta (un triangolo e' sempre circoscrivibile ad un cerchio) Da notare che , essendo congruenti i raggi HD, HE e HF ed essendo comune il segmento VH avremo che i tre triangoli VHD, VHE e VHF sono congruenti, cioe' le apoteme di una piramide retta sono sempre congruenti fra loro In figura, per non appesantire, ho disegnato completo solo il triangolo VHF 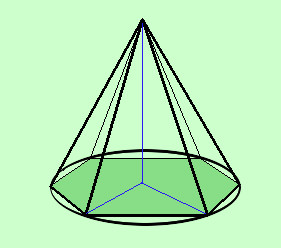 Diremo infine regolare una piramide retta che abbia come base un poligono regolare In tal caso tutte le facce laterali della piramide sono tra loro congruenti A destra una piramide esagonale regolare |

|

|

|

|