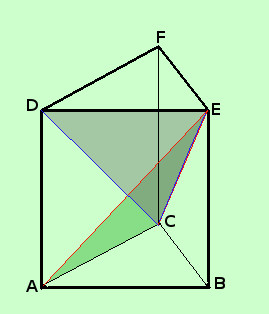
Teorema: Una piramide e' equiestesa alla terza parte di un prisma avente base equivalente e stessa altezza Facciamo la dimostrazione per una piramide triangolare (e quindi per un prisma triangolare) per le piramidi con altra base bastera' applicare il principio di Cavalieri (vedi figura a pagina precedente) IPOTESI: ABCE piramide TESI: Vol(ABCE) = 1/3 Vol(ABCDEF) Dividiamo il prisma in 3 tetraedri: DCEF, DCEA e ABCE(la nostra piramide) Consideriamo i due tetraedri DCEF e DCEA: essi hanno la stessa base DCE ed inoltre le altezze condotte da F ed A sul piano DCE sono congruenti, quindi i due tetraedri, avendo basi equivalenti ed altezze uguali hanno stesso volume Consideriamo poi i tetraedri DCEA e ABCE: essi hanno la stessa base ACE ed inoltre le altezze condotte da D e B sul piano ACE sono congruenti, quindi i due tetraedri, avendo basi equivalenti ed altezze uguali hanno stesso volume Di conseguenza i tre tetraedri sono tra loro equiestesi e quindi uno di loro e' equiesteso alla terza parte del prisma; allora la piramide ABCE e' equiestesa alla terza parte del prisma ABCDEF, come volevamo |

|

|

|

|