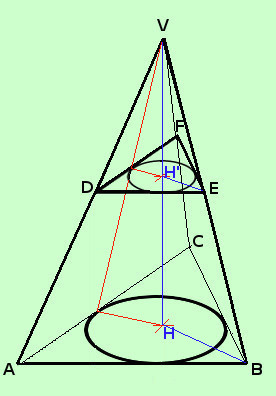
Approfondimento sulla proporzionalita' Sappiamo gia' dalla geometria piana che nei poligoni simili le aree stanno fra loro come i quadrati dei lati, delle altezze, delle apoteme corrispondenti Ad esempio nel tronco di piramide considerato in figura avremo As(ABC) : As(DEF) = AB2 : DE2 = BC2 : EF2 = CA2 : FD2 Possiamo estendere la proprieta' nello spazio (lo facciamo pero' senza dimostrazione per ora) dicendo che nello spazio vale la proprieta': Se due solidi sono simili allora i volumi stanno fra loro come i cubi delle relative altezze, apoteme, lati corrispondenti I due solidi in figura, intuitivamente, sono simili perche' i piani su cui poggiano le basi ABC e DEF sono paralleli, quindi e' valido il teorema di Talete nello spazio In figura ti ho tracciato alcuni triangoli simili: in rosso quelli per le apoteme ed i raggi, in blu quelli per le altezze e gli spigoli Cioe' ad esempio nella figura a fianco avremo Vol(VABC) : Vol(VDEF) = VH3 : VH'3 Vol(VABC) : Vol(VDEF)= AB3 : DE3 = .... In particolare, per calcolare il volume del tronco di piramide, utilizzeremo la proporzione fra le aree e le altezze che, utilizzando la figura a fianco, potremo scrivere nel seguente modo As(ABC) : As(DEF) = VH2 : VH'2