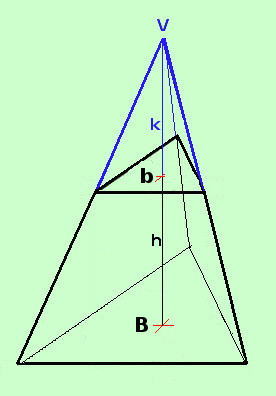
Consideriamo il tronco di piramide di base maggiore B, di base minore b e di altezza h Per semplicita' chiamiamo B sia la base maggiore che la misura dell'area della base stessa, lo stesso vale per b Come dati ho le misure delle aree di base e quello dell'altezza h quindi devo trovare la formula finale solamente con questi dati Prolungo il tronco di piramide fino ad ottenere il vertice V e considero le due piramidi di vertice V la prima di base B ed altezza h+k la seconda (quella sopra) di base b ed altezza k Per calcolare il volume del tronco di piramide faro' la differenza fra il volume della piramide maggiore e quello della piramide minore Per semplicita' chiamo VM il volume della piamide maggiore e Vm il volume della piramide minore e q l'altezza della piramide maggiore (q=h+k) Ho VM = B·q /3 e Vm = b·k /3 Vtronco = B·q /3 - b·k /3
Applichiamo la proporzione indicata nella pagina precedente fra le aree e le altezze: posso scrivere B : b = q2 : k2 Per la proprieta' del permutare scrivo B : q2 = b : k2 = d Ho chiamato d il valore del rapporto di proporzionalita' Qindi posso ricavare B e b B = d q2 e b = d k2 Sostituendo nella formula del volume ottengo
evidenzio d/3
scompongo: (differenza di cubi)
ed essendo q-k = h
riporto d dentro parentesi
Ma dal calcolo B = d q2 e b = d k2 fatto sopra so che vale dq2 = B e dk2 = b inoltre, moltiplicando B·b ottengo B·b = d2q2k2 ed, estraendo la radice e leggendo alla rovescia
Stavolta leggere la formula non e' molto semplice: comunque, se a qualcuno interessa occorre fare riferimento alla proporzione continua (quella che ha i termini medi identici B : x = x : b) in modo che ricavando x (termine medio proporzionale) ottengo Il volume di un tronco di piramide di altezza data e' uguale al volume di 3 piramidi aventi la stessa altezza, la prima avente come base la base maggiore del cono, la seconda avente come base l'area di un poligono medio proporzionale fra le due basi e la terza avente come base la base minore del tronco dato Facciamo un semplice esecizio: Calcolare il volume di un tronco di piramide avente base maggiore di area 12m2, base minore di 3 m2, alto 2 metri Applichiamo la formula
Quindi il nostro tronco di piramide ha un volume di 24 metri cubi |

|

|

|

|