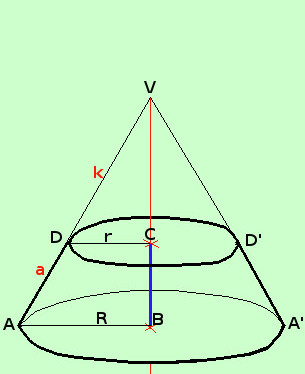
 Per calcolare la superficie del tronco di cono prolunghiamone la superficie fino a ricostruire il cono VAA' e poi calcoliamone la superficie laterale come differenza fra le superfici laterali dei coni VAA' e VDD' Asl(DAA'D') = Asl(VAA') - Asl(VDD') Essendo dati a: apotema del tronco di cono, R: raggio della circonferenza di base maggiore ed r: raggio della circonferenza di base minore, chiamiamo k l'apotema del cono piccolo, quindi a+k e' l'apotema del cono VAA' Asl(VAA') = πR (a+k) Asl(VDD') = πr k quindi Asl(DAA'D') = πR (a+k) - πr k = πRa + πRk - πrk = = πRa + πk(R - r) Ora, per trovare la formula, dovremo esprimere k con i dati che abbiamo, cioe' mediante R, r ed a; per fare questo consideriamo i triangoli simili VAB e VDC essi hanno AVB = DVC^^ perche' in comune ABV = DCV^^ perche' retti Quindi, avendo due angoli congruenti, per il primo criterio di similitudine i due triangoli sono simili e posso scrivere AV : DV = AB : DC (a+k) : k = R : r applico la proprieta' dello scomporre per poter avere una sola k nell'espressione (a+k-k) : k = (R-r) : r a : k = (R-r) : r ricavo k: essendo k un medio devo fare il prodotto degli estremi fratto l'altro medio
sostituisco questo valore nella formula della superficie laterale ed ottengo
Da notare che, se sostituiamo le circonferenze con i perimetri abbiamo che la formula e' la stessa che valeva per il tronco di piramide: infatti alla stessa formula potevamo arrivare considerando un tronco di piramide regolare ed aumentandone il numero dei lati: man mano che i lati aumentano la misura del perimetro di base si avvicina alla misura della lunghezza della circonferenza Per avere la superficie totale bastera' aggiungere le due aree di base
|

|

|

|

|