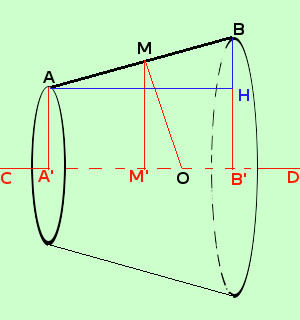
 M e' il punto medio di AB O e' il punto di intersezione dell'asse del segmento AB con l'asse di rotazione CD In pratica in questo caso si tratta di un tronco di cono di altezza A'B', apotema AB e raggi AA' e BB' quindi abbiamo, per la superficie di rotazione Area laterale = π AB · (AA' + BB') Considero il trapezio AA'B'B, traccio per M la parallela a BB', ottengo MM'; essendo M il punto medio di AB ne deriva che M' e' il punto medio di A'B' e che MM' = (AA'+BB')/2 E' una dimostrazione piuttosto semplice che potresti fare come esercizio; se vuoi puoi vedere qui la dimostrazione nella formula di partenza moltiplico e divido per 2 (tanto non cambia niente) per poter operare la sostituzione Area laterale = 2 π AB · (AA' + BB')/2 = 2 π AB · MM' Ora considero i triangoli MM'O e AHB essi hanno: MM'O=AHB ^ ^ perche' retti M'MO=HAB ^ ^ perche'angoli con lati fra loro perpendicolari M'M⊥AH e MO⊥AB Allora i tre angoli sono uguali ed essendo MOM' simile a AHB, per il primo criterio di similitudine, posso scrivere la proporzione MM' : AH = OM : AB so che AH = A'B' MM' : A'B'= OM : AB applico la proprieta' fondamentale (prodotto dei medi uguale al prodotto degli estremi) AB·MM' = MO·A'B' sostituiamo nell'espressione dell'area trovata prima Area laterale = 2 π AB · MM' = 2π MO · A'B' cioe' Area laterale = 2π OM · A'B' come volevamo |