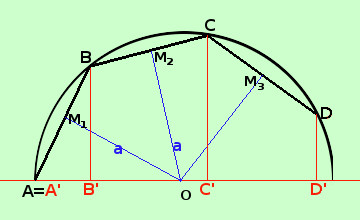
Area della superficie di rotazione di una poligonale regolare Chiamiamo poligonale regolare parte del perimetro di un poligono regolare Dimostriamo che vale il teorema L'area della superficie generata dalla rotazione completa di una poligonale regolare attorno ad un asse passante per il centro del poligono e non tagliante la poligonale vale il prodotto della circonferenza di raggio l'apotema della poligonale per la proiezione della poligonale sull'asse Dimostrazione: Notiamo che M e' il punto medio di ogni segmento ed MO e' l'asse del segmento stesso, inoltre le apoteme, essendo la poligonale regolare, sono tutte uguali OM1 = OM2 = OM3 = a Per il teorema dimostrato nella pagina precedente abbiamo che la superficie di rotazione generata da AB vale: Area = 2 π OM1·A'B' = 2 π a ·A'B' la superficie di rotazione generata da BC vale: Area = 2 π OM2·B'C' = 2 π a·B'C' la superficie di rotazione generata da AB vale: Area = 2 π OM3·C'D' = 2 π a·C'D' Quindi la superficie di rotazione della poligonale regolare vale la somma delle varie superfici Area = 2 π a A'B' + 2 π a B'C' + 2 π a·C'D' = 2a π (A'B'+B'C'+C'D')= 2a π (A'D') cioe' Area = 2a π (A'D') come volevamo.