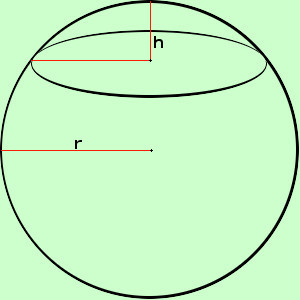
 la formula e' molto semplice; Invece per la dimostrazione bisogna scomodare il calcolo integrale e qui non la facciamo Acalotta sferica = 2 π r h
Da notare che nella formula compare solamente il raggio r della sfera e non il raggio della circonferenza di base della calotta Da notare anche che, utilizzando il teorema di Pitagora, e' possibile scrivere una relazione fra h altezza della calotta, o meglio, del segmento sferico ad una base 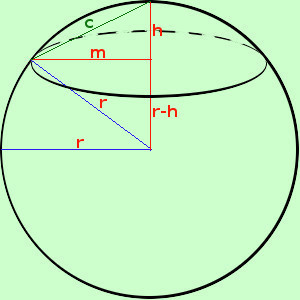 r raggio della sfera
r raggio della sferam raggio della circonferenza di base della calotta r2 = m2 + (r-h)2 sviluppando ottengo r2 = m2 + r 2 - 2rh + h2 porto 2rh prima dell'uguale e tutti gli altri termini dopo l'uguale 2rh = -r2 + m2 + r 2 + h2 2rh = m2 + h2 e quindi, sostituendo nella formula dell'area ho la formula equivalente Acalotta sferica = π (m2 + h2) Inoltre in qualche testo ho visto, introducendo il valore c corda dell'arco generatore la formula Acalotta sferica = π c2 infatti per il teorema di Pitagora c2 = m2 + h2 L'arco con corda c e' l'arco generatore perche' facendogli fare un giro completo attorno ad h ottengo la calotta sferica approfondire? |

|

|

|

|