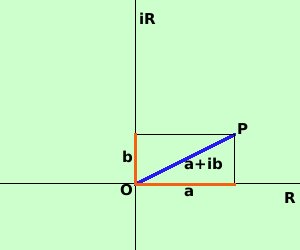
 Consideriamo un numero complesso, cioe' a+ib formato da una parte
reale piu' una parte immaginaria e consideriamolo come segmento nel piano
complesso
la prima cosa che e' evidente e' che si tratta
di un numero composto di due parti fra loro indipendenti nel senso che una parte
e' un normale numero reale e l'altra ha una parte i che la rende
diversa dalla prima.
Consideriamo un numero complesso, cioe' a+ib formato da una parte
reale piu' una parte immaginaria e consideriamolo come segmento nel piano
complesso
la prima cosa che e' evidente e' che si tratta
di un numero composto di due parti fra loro indipendenti nel senso che una parte
e' un normale numero reale e l'altra ha una parte i che la rende
diversa dalla prima.Quindi potrei anche rappresentare il numero complesso OP = a+ib come la coppia P = ( a, b) considerando che il numero a si trova sulla retta reale R mentre il numero b si trova sulla retta immaginaria iR, cioe' considerare il numero complesso come una coppia di numeri in cui il primo appartiene ad R ed il secondo ad iR 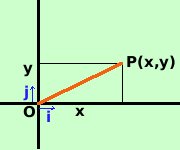 questo modo di pensare un punto e' abbastanza comune in matematica: basta pensare al piano cartesiano ed alla rappresentazione di un punto mediante le coordinate; pero' invece di considerare il punto P consideriamo il segmento OP (vettore) P = ( x, y) ma posso anche pensare OP = xi+yj con i e j segmenti unitari il primo sull'asse x ed il secondo sull'asse y 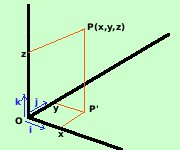 come l'abbiamo fatto per il piano possiamo farlo per lo spazio: rappresentiamo un punto P mediante le cooordinate P(x,y,z) e consideriamo il segmento OP. P = ( x, y, z) ma posso anche pensare OP = xi+yj +zk con i, j e k segmenti unitari il primo sull'asse x, il secondo sull'asse y ed il terzo sull'asse z I vari segmenti OP, qui sopra considerati, sono dei vettori |

|

|

|

|