.

Un esempio per capire meglio Non sono concetti semplici, quindi vediamo di sviluppare un esempio, il piu' semplice possibile che ci permetta di vedere in pratica come si costruisce la distribuzione cercata: consideriamo un evento tale che la probabilita' e la sua probabilita' contraria abbiano lo stesso valore, ad esempio l'uscita di testa nel lancio di una moneta Sviluppiamo problemi diversi per diversi valori di n Nella prima riga scrivo le varie combinazioni che possono uscire e nella seconda il numero di tali combinazioni, nella terza il valore della probabilita' dell'evento ed, a destra, la rappresentazione grafica con, in verticale, il numero delle combinazioni possibili probabilita' di uscita di testa nel lancio di una moneta S1 T C 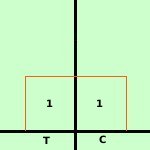1 1 1/2 1/2 probabilita' di uscita di testa nel lancio di due monete S2 TT TC    CT CC 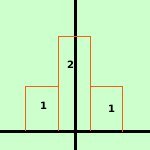1 2 1 1/4 2/4 1/4 probabilita' di uscita di testa nel lancio di tre monete S3 TTT TTC    TCT    CTT CCT    CTC    TCC CCC 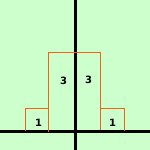1 3 3 1 1/8 3/8 3/8 1/8 probabilita' di uscita di testa nel lancio di quattro monete S4 TTTT TTTC    TTCT TCTT    CTTT TTCC    TCTC    CTTC CCTT    CTCT    TCCT CCCT    CCTC CTCC    TCCC CCCC 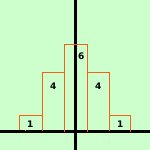1 4 6 4 1 1/16 4/16 6/16 4/16 1/16 probabilita' di uscita di testa nel lancio di cinque monete S5 TTTTT TTTTC TTTCT TTCTT TCTTT CTTTT TTTCC   TTCTC TCTTC   CTTTC TCTCT   CTTCT CTCTT   CCTTT TTCCT   TCCTT CCCTT   CCTCT CTCCT   TCCCT CTCTC   TCCTC TCTCC   TTCCC CCTTC   CTTCC CCCCT CCCTC CCTCC CTCCC TCCCC CCCCC 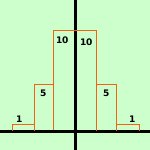1 5 10 10 5 1 1/32 5/32 10/32 10/32 5/32 1/32 Osserviamo due fatti importanti: Se sostituisco ai numeri delle combinazioni i valori delle probabilita' i grafici vanno bene lo stesso: in tal caso l'area di ogni rettangolo corrisponde alla probabilita' dell'evento e la somma di tutte le aree deve sempre dare come risultato 1. I numeri che abbiamo trovato corrispondono ai valori del triangolo di Tartaglia e quindi i nostri valori corrispondono ai coefficienti delle potenze del binomio Se hai bisogno di ripassare nei particolari il Triangolo di Tartaglia