.

Distribuzione binomiale (o di Bernoulli) Quanto fatto alla pagina precedente ci porta alla formula per calcolare la variabile aleatoria. 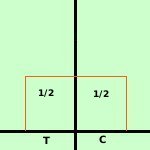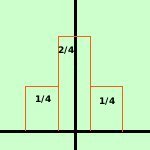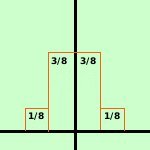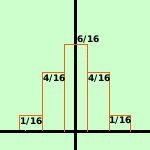Facciamolo prima su un esempio Trovare le varie probabilita' di "uscita di testa" nel lancio di 5 monete Dobbiamo trovare la formula per calcolare i seguenti valori delle singole probabilita' della variabile aleatoria S5 n° uscita teste 5 teste 4 teste 3 teste 2 teste 1 testa 0 teste probabilita' 1 ----- 32 5 ----- 32 10 ----- 32 10 ----- 32 5 ----- 32 1 ----- 32 Per trovarle sara' sufficiente considerare i fattori dello sviluppo della potenza quinta del binomio; p e' la probabilita' di uscita di testa per una moneta (1/2) e q e' la sua probabilita' contraria (sempre 1/2) (p+q)5 = k=0,1,2,3,4,5 ( 5 k ) · pk · q5-k = = 1·(1/2)5 · (1/2)0 + 5·(1/2)4 · (1/2)1 + 10 ·(1/2)3 · (1/2)2 + 10·(1/2)2 · (1/2)3 + 5·(1/2)1 · (1/2)4 + 1·(1/2)0 · (1/2)5 = = 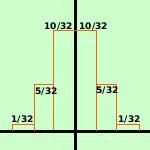1/32 + 5/32 + 10/32 + 10/32 + 5/32 + 1/32 Possiamo quindi generalizzare la formula per calcolare la probabilita' di uscita di testa k volte su n prove effettuate considerandola come il termine della potenza del binomio (p-q)n che ha il termine p a potenza k Probabilita' = ( n k ) · pk · qn-k Questi valori considerati al variare di k forniscono una variabile aleatoria la cui rappresentazione e' detta anche distribuzione binomiale (corrispondendo allo sviluppo della potenza del binomio) od anche distribuzione di Bernoulli 1 moneta (a+b)1 2 monete (a+b)2 3 monete (a+b)3 4 monete (a+b)4 5 monete (a+b)5 Tutte le aree delle distribuzioni binomiali, somma dei rettangoli, essendo somma di probabilita', valgono 1 All'aumentare del numero di lanci effettuati le distribuzioni binomiali si avvicinano ad una curva detta curva a campana o curva di Gauss     (fare link) Una variabile aleatoria di tipo binomiale viene anche detta brevemente variabile binomiale e la indicheremo con la lettera S Le probabilita' p e q possono anche essere diverse: vedi questo esempio