.

Dal discreto al continuo Esistono vari tipi di problemi in cui l'insieme dei valori possibili e' continuo, cioe' abbiamo un numero infinito di probabilita' per tutti i valori compresi in un intervallo in corrispondenza biunivoca con un intervallo della Retta Reale Esempi: la probabilita' di caduta di un satellite su una zona dell'Europa So solamente che cadra' in una certa zona con probabilita' p, ma non posso indicare un punto o un numero finito di punti in cui puo' cadere l'usura di un cilindro ruotante in un meccanismo posso indicare il raggio massimo ed il raggio minimo che mi permette di usarlo, ma non posso suddividere la differenza dei raggi in un numero finito di punti La probabilita' di morire di una persona di sesso maschile di 50 anni da oggi al 2070 Serve per calcolare le tabelle assicurative, ma non posso indicare il valore preciso della probabilita' di morte istante per istante Quelli sopra sono tutti esempi di probabilita' continua; in alcuni casi si puo' ovviare, come nel caso delle assicurazioni, dividendo l'intervallo in anni, pero' e' un'approssimazione: la probabilita' di morte di una persona a gennaio sara' diversa dalla probabilita' per la stessa persona a dicembre dello stesso anno. Consideriamo ancora la caduta di un oggetto su un piano determinato: come posso esprimere la probabilita' di impatto in un punto se un punto non ha dimensione? Allora dovro' sostituire al concetto di punto il solito concetto di intervallo per poter trovare una probabilita' effettiva: e' lo stesso ragionamento che ci ha portato a costruire l'analisi matematica basandola sul concetto di intervallo; Se considero un intervallo, anche se infinitesimo, allora per esso potro' parlare della probabilita' di impatto con l'oggetto che cade Per sapere come comportarci intuitivamente riferiamoci ad un esempio classico: lanciando una moneta ho due possibilita': o testa o croce entrambe con probabilita p = ½ Abbiamo gia' studiato questo caso e visto la distribuzione di questo fenomeno vedi l'esempio Se aumentiamo il numero delle prove avremo che al posto dei rettangoli avremo dei rettangoli sempre piu' snelli sino ad arrivare a basi infinitesime e quindi ad avere, per i valori delle probabilita', una curva indistinguibile da una curva continua 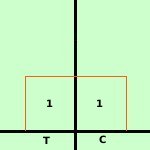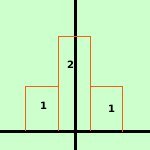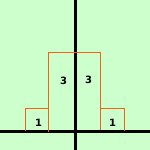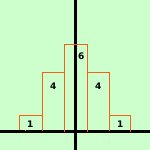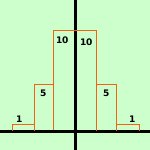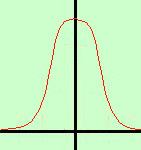Dovremo quindi di utilizzare l'analisi matematica e lo studio di funzioni, inoltre, siccome le probabilita' saranno legate alle aree di parti delle curve, dovremo conoscere bene soprattutto il calcolo degli integrali definiti