.

Funzione di ripartizione Particolare importanza, nel caso continuo, ha la funzione di ripartizione (somma di tutte le probabilita' precedenti una probabilita' data) In generale, data la probabilita' P(x) nell'intervallo chiuso [a;b] potremo definire come funzione di ripartizione su ℜ una funzione y = F(x) tale che 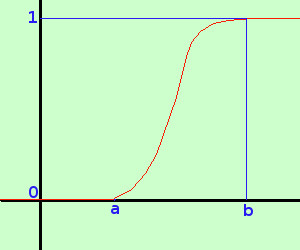Sia definita per ogni valore di x in ℜ Assuma valori compresi fra 0 ed 1 essendo F(x) = 0 per x ≤ a F(x) = 1 per x ≥ b La funzione e' monotona non decrescente (cioe' o cresce o si mantiene costante in ogni intervallo considerato) La funzione di ripartizione servira' in quei problemi che coinvolgano i segni di ≤ e ≥ Per semplicita' consideriamo solamente casi in cui la variabile aleatoria e' continua (generalmente e' cosi' ma si hanno delle eccezioni che non consideriamo)