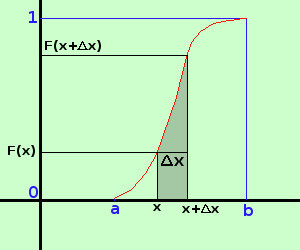
 Se ora passiamo al limite per Δx →0 avremo la definizione di derivata
Se ora passiamo al limite per Δx →0 avremo la definizione di derivata
La funzione f(x) = F'(x) si chiama densita' di probabilita' o semplicemente funzione di densita' Da notare che la funzione di densita' f(x) non esprime una probabilita' (es. la tangente alla curva in figura puo' anche avere coefficiente angolare superiore ad 1) pero' essa serve a calcolare una probabilita': se considero il differenziale di F(x) dF(x) = F'(x) = f(x)dx esso coincide con la derivata della funzione a meno di infinitesimi di ordine superiore dF(x) = F'(x) + εx = f(x)dx e quindi, essendo f(x)dx il prodotto fra la funzione densita' ed il differenziale dx allora f(x)dx e' la probabilita' che la variabile casuale assuma un valore compreso nell'intervallo infinitesimo x ed x+dx a meno di infinitesimi di ordine superiore a dx Cerchiamo di capirci meglio | .

|

|

|

|