studio intuitivo della funzione data Studiamo la funzione F(x) = 0               se x < 0 1 - e-αx        se x≥0 seguiamo alcuni punti dello schema proposto in analisi Determinazione del campo di esistenza: nel nostro caso il campo di esistenza e' tutto ℜ perche' per x≤0 la nostra funzione vale sempre zero e quindi e' sempre definita; anche per x >0 e' sempre definita (cioe' per ogni valore reale sostituito ad x la mia funzione assume un valore reale) Determinazione del tipo di funzione E' una funzione formata da due diverse funzioni: per x≤0 e' una funzione costante (e quindi il grafico si riduce all'asse negativo delle x) e questa non c'e' bisogno di studiarla per x >0 invece e'la differenza fra una funzione costante ed una di tipo esponenziale (d'ora in avanti ci limiteremo a studiare solamente il ramo della funzione x >0) Intersezione con gli assi Se considero l'asse y, cioe' pongo x=0 allora la funzione vale y = 1 - e-αx = 1 - e -α(0) = 1 - e 0 = 1-1 = 0 Quindi O≡(0;0) e' un punto della funzione Valori agli estremi del campo di esistenza e asintoto orizzontale I punti in questione sono dati dai tre valori per le x x = -∞ in tal caso la funzione vale 0 x = 0 abbiamo gia' visto che allora y=0 x = +∞ in tal caso abbiamo limx→+∞ [1 - e-α·(x)] → 1 - e-∞ = 1-0 = 1 allora y = 1 e' l'asintoto orizzontale (retta a cui tende la funzione senza mai raggiungerla) 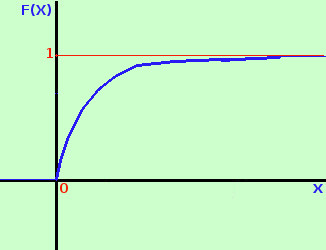Positivita' e negativita', crescenza e decrescenza Considero la funzione y = 1 - e-αx e ne faccio la derivata y ' = 0 + αe-αx y ' = αe-αx Y' e' sempre positiva perche' α e' un termine positivo e l'esponenziale e' definito sempre positivo; essendo la derivata prima sempre positiva la funzione e' sempre crescente Derivata seconda e concavita' faccio la derivata seconda y''= -α2 e-αx essendovi il meno davanti ad un quadrato la derivata e' sempre negativa, quindi la concavita' e' rivolta verso il basso a destra la rappresentazione grafica