|
Riprendiamo un esempio gia' accennato: Consideriamo ancora la variabile gaussiana discreta sull'esempio del lancio di una moneta: lanciando una moneta consideriamo la probabilita' che esca testa: ho la probabilita' p = ½ e la probabilita' contraria q=½ All'aumentare del numero delle prove avremo che successivi rettangoli obbediranno alla legge del triangolo di tartaglia, essendo legati alla regola della potenza del binomio
quindi, poiche' l'area sottesa deve sempre valere 1 (somma di tutte le probabilita'), al posto dei rettangoli avremo dei rettangoli sempre piu' snelli sino ad arrivare a basi infinitesime e quindi ad avere, per i valori delle probabilita', una curva indistinguibile da una curva continua 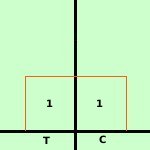
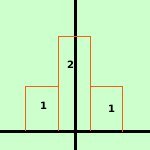
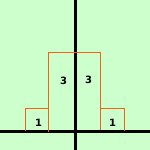
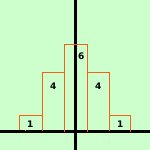
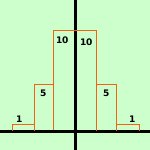
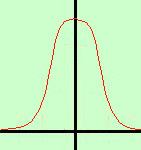 Tale curva sara' detta anche curva a campana di Gauss e sara' del tipo y = ke-x2 con k valore dato La dimostrazione analitica di come si ricavi la formula precisa trascende i limiti dei programmi delle scuole medie superiori, quindi, nelle prossime pagine, ci accontenteremo di prendere la formula finale e di fare alcune osservazioni | .

|

|

|

|