.

Studio della variabile casuale gaussiana standardizzata Standardizzata implica che non dipende dall'unita' di misura della variabile Come esercizio, anche per ripassare un po' di Analisi, e per ricavarne le proprieta' studiamo la funzione f(x) = 1 √(2π) e-½x2 f(x) = 1 √(2π) e-½x2 Seguiamo lo schema che abbiamo visto in Analisi. Per i nostri calcoli sappiamo che la costante 1/ √(2π) vale circa 0,3989 Determinazione del campo di esistenza Il campo di esistenza e' tutto ℜ Determinazione del tipo di funzione intanto posso dire che e' una funzione pari perche' se sostituisco x con -x non cambia niente (-x)2 = x2, quindi la funzione sara' simmetrica rispetto all'asse delle y Intersezioni con gli assi Vediamo se esistono intersezioni con l'asse y faccio il sistema fra la funzione e l'asse y y = 1/√(2π) e-½x2 x = 0 y = 1/√(2π) e-½02 x = 0 essendo e0 = 1 y = 1/√(2π) ≅ 0,3989 x = 0 Quindi la curva taglia l'asse delle y nel punto A≡(0; 1/√(2π) ) ≅(0; 0,3989) Vediamo ora se esistono intersezioni con l'asse x faccio il sistema fra la funzione e l'asse x y = 1/√2π e-½x2 y = 0 1/√(2π) e-½x2 = 0 x = 0 essendo e-½x2 un esponenziale sara' senpre maggiore di zero, ed essendo 1/√(2π) una costante allora il termine non sara' mai zero, quindi La curva non taglia l'asse delle x Valori agli estremi del campo di esistenza Siccome il campo di esistenza va da -∞ a + ∞ allora dovremo trovare tali valori con gli asintoti Positivita' e negativita' Risolvo la disequazione 1/√(2π) e-½x2 > 0 essendo 1/√(2π) una costante positiva basta risolvere e-½x2 > 0 questo essendo un esponenziale e' sempre positivo la funzione e' sempre positiva (il grafico sara' tutto sopra l'asse delle x) Determinazione degli asintoti Non possono esistere asintoti verticali (la funzione non diventa infinita per valori finiti di x) Ricerca di eventuali asintoti orizzontali od obliqui limx→-∞1/√2π e-½x2 = e-∞ = 0 limx→+∞1/√2π e-½x2 = e-∞ = 0 quindi l'asse delle x e' un asintoto orizzontale y = 0 asintoto orizzontale ed essendo la curva sempre positiva la curva si avvicina all'asintoto da sopra Determinazione della derivata prima Eseguiamo la derivata prima 1/√(2π) e' una costante quindi resta davanti al risultato e-½x2 e' una funzione (esponenziale) di funzione ( esponente -½x2) derivata dell'esponenziale e-½x2 derivata dell'esponente -½ ·2x = -x Quindi ho la derivata y ' = - x √(2π) e-½x2 Crescenza e decrescenza Poniamo la derivata prima maggiore di zero per vedere dove e' positiva (funzione crescente) o negativa (funzione decrescente) - x √(2π) e-½x2 > 0 essendo 1/√(2π) una costante positiva posso scrivere - x e-½x2 > 0 l'esponenziale e' sempre positivo, quindi scrivo - x > 0 ed ottengo x < 0 La derivata e' positiva per x < 0 ed e' negativa per x > 0, quindi la funzione e' crescente per x < 0 ed e' decrescente per x > 0 Determinazione dei massimi e minimi senza risolvere equazioni, essendo la funzione crescente per x < 0 e decrescente per x > 0 allora il punto corrispondente ad x=0 e' un massimo Corrisponde al punto A di intersezione con l'asse y A = M ≡(0; 1/√(2π) ) ≅(0; 0,3989) Determinazione della derivata seconda eseguiamo la derivata della derivata prima: non considerando la costante 1/√(2π) e' un prodotto di funzioni -x ed e-½x2, quindi y '' = 1/√(2π)[ -1 ·e-½x2 -x ·(- x e-½x2)] y '' = 1/√(2π)[ -1 ·e-½x2 + x2 e-½x2)] y '' = 1/√(2π)[ e-½x2 ( x2 - 1)] ottengo y '' = x2-1 √(2π) e-½x2 Concavita' convessita' e flessi pongo la derivata seconda uguale a zero x2-1 √(2π) e-½x2 = 0 essendo √(2π) una costante ed essendo l'esponenziale per definizione sempre positivo la mia equazione si riduce a x2-1 = 0 ottengo quindi due soluzioni x = -1 ed x = 1 ora studio il segno della mia funzione x2-1 √(2π) e-½x2 > 0 anche qui, essendo √(2π) una costante ed essendo l'esponenziale per definizione sempre positivo la mia disequazione si riduce a x2-1 > 0 essendo le soluzioni -1 ed 1 la mia disequazione e' verificata per valori esterni _____________ -1 _____________ +1 _______________  + + + + +     0 - - - - - - - - - - -   0    + + + + + + + Quindi posso dire che Da -∞ a -1 la concavita' e rivolta verso l'alto da -1 ad 1 la concavita' e rivolta verso il basso da 1 a +∞ la concavita' e' rivolta verso l'alto inoltre posso dire che per x=-1 e per x=1 avremo due flessi: calcoliamo il valore dei punti di flesso per x = -1 abbiamo y = 1/√(2π) e-½(-1)2 = 1/√(2π) e-½ per x = 1 abbiamo y = 1/√(2π) e-½(1)2 = 1/√(2π) e-½ 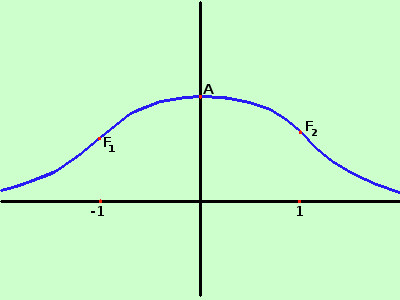Primo punto di flesso F1 ≡(-1; 1/√(2π) e-½) ≅ (-1; 0,2419) Secondo punto di flesso F2 ≡(1; 1/√(2π) e-½) ≅ (1; 0,2419) Ci accontentiamo dei punti di flesso senza fare ulteriori calcoli (complicati) per individuare le equazioni delle tangenti di flesso A destra il grafico della nostra funzione, per rappresentarla meglio l'unita' di misura sulle y e' diversa da quella sulle x Siccome nella forma richiama una campana e' chiamata anche "Curva a campana di Gauss"