|
Partiamo da un semplice esempio: supponiamo che io debba trovare la misura della lunghezza di una parete di una stanza con la precisione di un millimetro; mi procuro un doppio decimetro e comincio a misurare: trovo che le misure che ottengo mi danno risultati fra loro leggermente diversi. Secondo la teoria degli errori, scartando gli errori sistematici, cioe' quelli dovuti agli strumenti di misurazione o ad un modo errato di misurare, avro' che in ogni misura esiste un errore casuale che mi fornira' una misura piu' o meno grande della misura che cerco: se ora metto queste misure su un grafico e ripetendo il procedimento moltissime volte ottengo come rappresentazione proprio una curva a campana di Gauss e la misura migliore della parete sara' data dal vertice della campana. Intendiamoci: intuitivamente la misura centrale sara' solamente la misura che ha la piu' alta probabilita' di essere esatta, mentre per avere la probabilita' che la misura sia contenuta in un certo intervallo bastera' considerare l'area limitata dalla gaussiana, dall'asse delle x e dalle verticali mandate dai punti estremi dell'intervallo considerato. 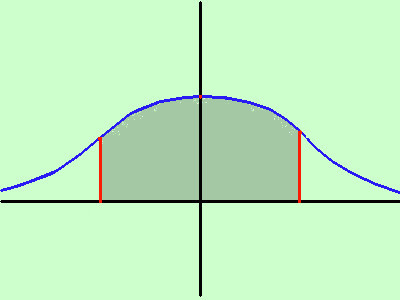 Come esempio considerate che l'area compresa fra le verticali passanti per i punti di flesso corrisponde a circa il 70% di probabilita' che la misura sia compresa in quell'intervallo (con piu' precisione circa il 68,27%) Cioe' la curva a campana di Gauss descrive il modo in cui gli errori casuali si distribuiscono quando facciamo una qualunque misura Siccome in quasi tutte le scienze il concetto di misura e' centrale (pensa alla statistica, alla fisica,...) abbiamo l'importanza che assume la curva a campana di Gauss Vista l'importanza della variabile casuale Gaussiana essa viene spesso indicata come variabile casuale normale | .

|

|

|