Rappresentazione grafica del montante ad interesse semplice Consideriamo la formula del montante ad interesse semplice M = C (1+i t) Consideriamola come M = C + C i t Per semplicita' considero il capitale C costituito da 1 euro, cosi' possiamo toglierlo dalla formula. Per avere poi il risultato finale per un capitale C bastera' moltiplicare quello che otteniamo per C M = 1 + i t Se cosideriamo fisso il tasso i abbiamo che il montante I dipende dal tempo t e tale dipendenza puo' essere rappresentata in un piano cartesiano come una retta nel piano di equazione y = m x + 1 con y uguale al Montante I x uguale al tempo t ed m (coefficiente angolare) uguale a i Quindi e' possibile rappresentare graficamente come varia l'interesse al variare del tempo e la rappresentazione grafica e' sempre data da una retta passante per il punto (0;1) Siccome il tempo non puo' andare all'indietro allora noi cosidereremo solamente il tempo positivo e quindi la semiretta che parte dal punto (0:1) Per disegnare subito il grafico basta osservare che corisponde alla formula dell'interesse vista nella pagina precedente aumentata di 1, quindi basta spostare verso l'alto tutto il grafico di 1 quindi il grafico di I = i t e' dato da 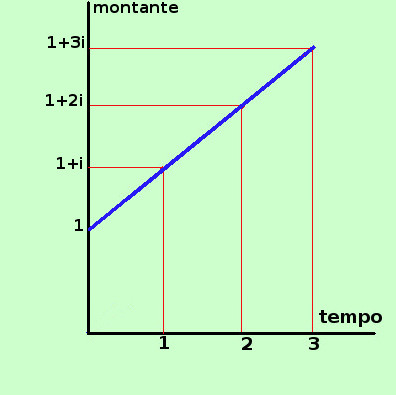Al'inizio (tempo 0) non avremo nessun interesse (se t=0 allora M= 1 + i·0 = 1) Al tempo 1 (dopo 1 anno) avremo il montante 1+i (se t=1 allora M = 1 + i·1 = 1+i) Al tempo 2 (dopo 2 anni) avremo il montante 1+2i (se t=2 allora M = 1 + i·2 = 1+2i) Al tempo 3 (dopo 3 anni) avremo il montante 1+3i (se t=3 allora M = 1 + i·3 = 1 + 3i) .......... Vediamo ora un esempio pratico Rappresentiamo graficamente l'interesse, sempre per un capitale di 1 euro impiegato al tasso del 2% (i = 0,02) 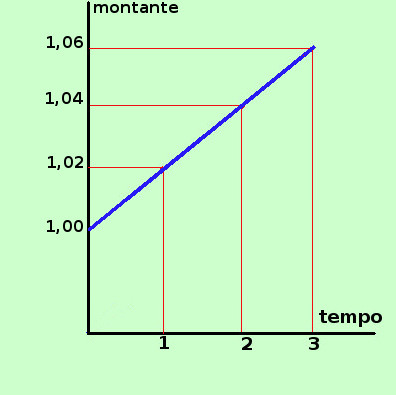Al'inizio (tempo 0) non avremo nessun interesse (se t=0 allora I= i·0 = 0) Al tempo 1 (dopo 1 anno) avremo l'interesse 0,02 cioe' 2 centesimi (se t=1 allora I= 0,02·1 = 0,02€) Al tempo 2 (dopo 2 anni)  avremo l'interesse 0,04 cioe' 4 centesimi (se t=2 allora I= 0,02·2 = 0,04€) Al tempo 3 (dopo 3 anni)  avremo l'interesse 0,06 cioe' 6 centesimi (se t=3 allora I= 0,02·3 = 0,06€) .......... Da notare che per farti vedere meglio il grafico in verticale ho messo lo spazio fra l'origine ed 1 molto inferiore a quello che sarebbe effettivamente, come ti ho gia' detto puoi fare queste cose, se non danno luogo ad equivoci, per poter evidenziare al meglio le cartteristiche del grafico che rappresenti Se il capitale e' diverso da 1 euro si procede in questo modo Rappresentiamo graficamente il montante, per un capitale di 1000 euro impiegato al tasso del 2% (i = 0,02) 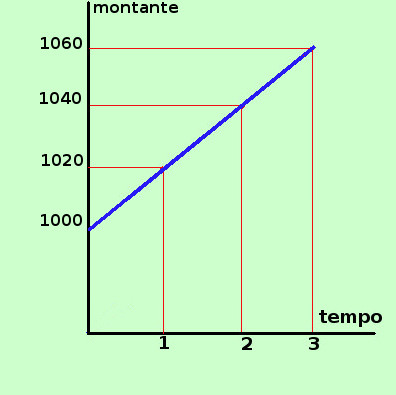Al'inizio (tempo 0) non avremo nessun interesse (se t=0 allora M= 1000·(1+i·0) = 1000,00€) Al tempo 1 (dopo 1 anno) avremo un montante di 1020 euro (se t=1 allora M = 1000·(1+0,02·1) = 1000·(1,02) = 1020,00€) Al tempo 2 (dopo 2 anni)  avremo un montante di 40 euro (se t=2 allora M= 1000·(1+0,02·2) = 1000·(1+0,04) = 1000·1,04 = 1040,00€) Al tempo 3 (dopo 3 anni)  avremo un montante di 60 euro (se t=3 allora M= 1000·(1+0,02·3) = 1000·(1+0,06) = 1000·1,06 = 1060,00€) ..........