|
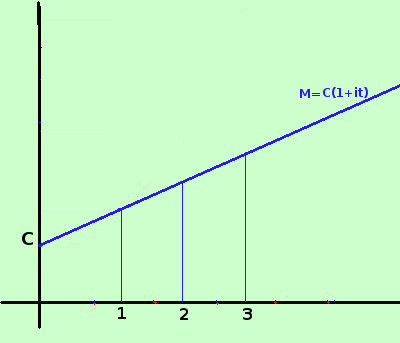
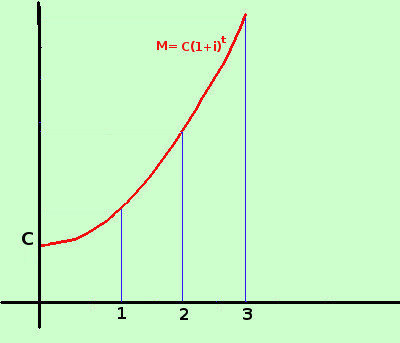
Considero i grafici della capitalizzazione lineare e composta
ora li metto a confronto ed ottengo 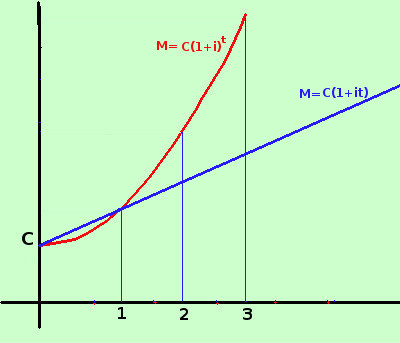 Come vediamo dal grafico per periodi inferiori ad un anno il grafico del montante ad interesse semplice e' superiore al grafico del montante ad interesse composto, allo scadere dell'anno i due montanti hanno lo stesso valore poi, proseguendo, il montante ad interesse composto cresce piu' del montante ad interesse sempice: si dice il montante ad interesse composto cresce in forma esponenziale il montante ad interesse semplice cresce in forma lineare (come una retta) Vediamo infine cosa significa, per tempi non interi, la capitalizzazione composta con la forma lineare e con la forma esponenziale 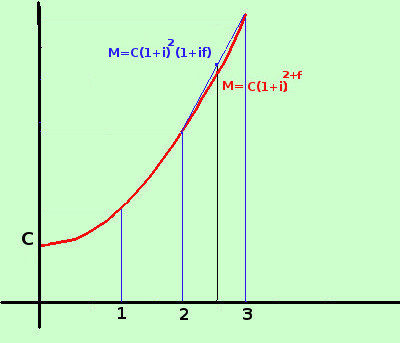 Mentra con la forma esponenziale calcoli il valore sulla curva rossa, nella forma lineare sostituisci l'ultimo tratto dell'esponenziale con un segmento e vai a calcolare il valore del montante su tale segmento, quindi avrai sempre che, calcolando il momtante con la formula lineare otterrai un valore superiore rispetto al montante calcolato esponenzialmente. Puoi anche dire che l'esponenziale ha la concavita' verso l'alto, quindi qualunque segmento di retta fra due suoi punti avra' valori superiori rispetto a quelli della curva (e la frazione di capitalizzazione lineare e' un segmento di retta) |

|

|

|

|