Calcolo del montante ad interesse composto per tempi interi con tasso non sulle tavole Si impiega il capitale di € 20000 per 18 anni ad interesse composto al 2,673%. Calcolarne il montante nei vari modi possibili e confrontare i risultati In questo caso abbiamo un numero di anni tale da farci scartare a priori il calcolo diretto, inoltre il tasso non e' sulla tavole Dati C = 20000,00 € t = 18 i = 2,60% = 0,02673 Eseguo l'esercizio nei vari modi possibili: Come gia' accennato scarto il metodo del calcolo del montante come prodotto di capitalizzazioni semplici perche' 18 anni renderebbero il calcolo troppo lungo Utilizzo la calcolatrice Imposto, sullo schermo il calcolo 20000·(1+0,02673)18 ottengo 32154,55687637 che approssimo a 32154,56 il montante e' di € 32154,56 utilizzo le tavole logaritmiche a 7 decimali Anche in questo esercizio calcolo solamente il fattore (1,02673)18 e poi moltiplichero' il risultato per il capitale M = 20000(1+0,02673)18 Calcolo il fattore (1+0,02673)18 coi logaritmi; per la proprieta' dei logaritmi ho Log (1,02673)18 = 18·Log 1,02673 = trasformo il numero in Logaritmo leggo sulle tavole logaritmiche a 7 decimali    10267,3 e' compreso fra 10267 e 10268 quindi devo fare l'interpolazione 10267,0      →    0114436    10267,3      →    0114436+x     423 10268,0      →    0114859    Di fianco ai due risultati trovi il numero 428 che corrisponde alla differenza fra i due valori trovati mentre la differenza fra il mio valore e quello minore e' 102673-102670 = 3 Nella tabella del 423 a 3 corrisponde 126,9 e questo e' il mio x quindi scrivo 0114436 + 126,9 = 0114562,9 = 01145629 la virgola ti indica solo come eseguire la somma Log 1,02673 = 0,01145629 Quindi Log (1+0,2673)18 = 18·Log(1,02673) = 18·0,01145629 = 0,20621322 Questo e' il logaritmo, ora trovo l'antilogaritmo (lo trasformo in valore normale) AntiLog 0,20621322 = Essendo la caratteristica 0 il valore dell'antilogaritmo sara' compreso fra 1 e 10, quindi avremo una cifra significativa prima della virgola la mia mantissa nella tavola a 7 decimali (20621322) non c'e'(il tempo 18 anni e' troppo elevato) e quindi considero 5 cifre 20621,322 e cerco fra i logaritmi normali leggo sulle tavole a 5 decimali e trovo 20602      →    20629    27 1607      →    1608    Di fianco ai due risultati trovi il numero 27 che corrisponde alla differenza fra i due valori della mantissa mentre la differenza fra il mio valore e quello minore e' 20621,322-20608 = 15,322 Nella tabella del 27 cerco 15,322; il numero minore piu' vicino e' 13,5 cui corrisponde la sesta cifra del nostro numero, cioe' 5 mi resta 15,322-13,5 = 1,822; sposto di un posto la virgola e cerco la settima cifra decimale Nella tabella del 27 cerco 18,22; siccome non prendero' altre cifre perche' l'errore supererebbe il valore della cifra trovata stavolta prendo la cifra piu' vicina il numero piu' vicino e' 18,9 cui corrisponde la settima cifra del nostro numero, cioe' 7 ottengo 160757 quindi scrivo Antilog 0,20621322 = 1,60757 e, calcolando il montante M = 20000·1,60757 = 32151,4 € il montante e' di € 32151,4 utilizzo le tavole del prontuario per il fattore (1+i)n stavolta il valore e' compreso fra due valori: tasso del 2,50% per 18 anni → 1,55965872 tasso del 2,75% per 18 anni → 1,62956973 per trovare il mio valore faccio l'interpolazione 0,02500      →    1,55965872    0,02673      →      1,55965872+x     0,02750      →    1,62956973    faccio la proporzione (1,62956973-1,55965872):0,00250 = x : (0,02673-0,02500) 0,06991101 : 0,00250 = x : 0,00173 x = 0,06991101 · 0,00173 0,00250 = 0,048378419 quindi ottengo (1.02673)18= (1,55965872+0,048378419) = 1,608037139 e quindi M = 20000·1,608037139 = 32160,7427784 €che approssimo a €32160,75 il montante e' di € 32160,75 In questo ultimo esercizio gli errori sono piuttosto rilevanti: il metodo migliore, che da' il risultato piu' preciso, comunque, e' sempre quello dell'utilizzo di una calcolatrice per calcoli finanziari, segue quello dell'uso dei logaritmi e quindi quello dell'interpolazione fra i tassi nelle tavole finanziarie che avra' sempre un errore dovuto all'utilizzo dell'interpolazione 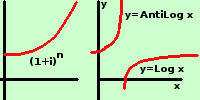L'errore e' dovuto all'interpolazione fra i tassi ed all'interpolazione per calcolare logaritmo ed antilogaritmo. Infatti la curva che rappresenta il tasso di interesse ha la concavita' rivolta verso l' alto e quindi avranno sempre un errore in eccesso Nel logaritmo abbiamo due interpolazioni diverse: La prima, nel passaggio dal numero al logaritmo avra' un errore in difetto, avendo la funzione logaritmo la concavita' rivolta verso il basso La seconda nel passaggio dal logaritmo al numero avra' un errore in eccesso avendo la funzione inversa del logaritmo (antilogaritmo) la concavita' rivolta verso l'alto Quindi con l'uso dei logaritmi i due errori in parte si compenseranno a vicenda