Tasso medio per piu' impieghi Supponiamo di avere piu'capitali impiegati con interesse diverso, il problema che ci poniamo e' come trovare il tasso per sostituire a tali capitali la loro somma riferendoci ad una scadenza comune Ho impiegato il capitale di 4000 € al tasso del 2,50% ed un altro di 5000 € al tasso del 3% a quale tasso dovrei impiegare il capitale totale di 9000 euro per avere lo stesso montante fra 6 anni? Dati: capitale1 = 4000€     i=0,025 capitale2 = 5000€     i=0,030 totale = 9000 €         i = x troviamo il tasso da applicare ai 9000 euro per avrre lo stesso risultato fra 6 anni Riporto tutti i dati alla scadenza, cioe' fra 6 anni Traccio la retta dei tempi 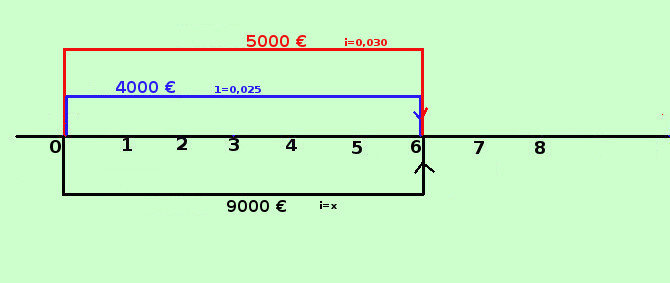Imposto l'equazione: 9000·(1+i)6 = 4000·(1+0,025)6 + 5000·(1+0,030)6 9000·(1+i)6 = 4000·(1,025)6 + 5000·(1,030)6 Per semplicita' divido tutto per 1000 9·(1+i)6 = 4·(1,025)6 + 5·(1,030)6 (1+i)6 = 4 · 1,0256 + 5 · 1,0306 9 = leggo sulle tavole e sostituisco = 4 · 1,15969342 + 5 · 1,19405230 9 = 1,178781687 per calcolare x conviene, sulle tavole, fare l'interpolazione rispetto ai tassi essendo il tempo uguale a 6 anni il mio valore e' compreso fra 1,17676836 che e' il tasso del 2,75% e 1,19405230 che e' il tasso del 3%, quindi il tasso che cerco sara' compreso fra 0,0275 e 0,030 1,17676836    →   0,0275     1,178781687   →   0,0275+x 1,19405230    →   0,030     imposto l'interpolazione: la differenza fra il terzo ed il primo valore sta alla differenza fra il terzo ed il primo tasso come la differenza fra il secondo ed il primo valore sta alla differenza fra il secondo ed il primo tasso (che e' x) (1,19405230-1,17676836):(0,030-0,0275)= (1,178781687-1,17676836):x (0,01728394):(0,0025)= (0,002013327):x x = 0,0025·0,002013327 0,01728394 = 0,000291214 Quindi il mio tasso sara' 0,0275+x = 0,0275+0,000291214 = 0,027791214 che approssimo a i = 0,0278 Quindi per avere lo stesso montante dovrei impiegare il capitale di 9000€ al tasso del 2,78%