calcolo del valore attuale di rendita differita

Calcolo del valore attuale di rendita differita

Consideriamo la rata fissa dell'importo di 1 €; per qualunque altro importo bastera' poi moltiplicare tale importo per il nostro risultato

Consideriamo sulla retta dei tempi una rendita immediata posticipata di rata 1 €, iniziante fra p anni e di durata n anni

i numeri sotto la retta indicano i periodi: essendo posticipata la rata e' pagata alla fine del periodo e la prima rata scade alla fine del periodo p+1

Il primo euro sara' versato alla fine del periodo p+1 e quindi dovra' essere spostato indietro nel tempo per p+1 anni, quindi alla fine avra' valore 1·(1+i)^-(p+1)€ = v^p+1
Il secondo euro sara' versato alla fine del periodo p+2 e dovra' essere spostato indietro nel tempo per p+2 anni quindi alla fine avra' valore 1·(1+i)^-(p+2)€ = v^p+2
...............................
...............................
Il penultimo euro sara' versato alla fine del periodo p+n-1 e dovra' essere spostato indietro nel tempo per p+n-1 anni quindi alla fine avra' valore 1·(1+i)^-(p+n-1)€ = v^p+n-1
L'ultimo euro sara' versato alla fine dell'ultimo periodo e dovra' essere spostato indietro nel tempo per p+n periodi quindi alla fine avra' valore 1·(1+i)^-(p+n)€ = v^p+n
per semplificare alla fine ho sottointeso gli €

Raccogliendo per calcolare il montante dovremo eseguire la somma
= v^p+1 + v^p+2 + ............... + v^p+n-1 + v^p+n
Tra tutti i termini metto in evidenza v^p
= v^p( v + v² + ............... + v^n-1 + vⁿ)
Si vede ora che, dentro parentesi si tratta del valore attuale di una rendita posticipata e quindi posso scrivere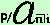
= v^p Cioe' posso dire:
il valore attuale di una rendita differita posticipata di p anni e' uguale al valore attuale di una rendita immediata posticipata con lo stesso periodo spostata indietro nel tempo per p anni
Basta guardare la retta dei tempi: se sposti indietro nel tempo la rendita per p anni attieni una rendita immediata posticipata di n periodi

=v^p ·

1 - vⁿ

i

Siccome abbiamo un prodotto possiamo rendere questa formula un po' piu' semplice per gli esercizi eseguendo la moltiplicazione e trasformando nel seguente modo

=v^p ·

1 - vⁿ

i

v^p - v^n+p

i

Al numeratore tolgo ed aggiungo 1 (posso farlo perche' non mi cambia il valore dell'espressione)

v^p -1 + 1 - v^n+p

i

1 - v^n+p + v^p -1

i

Ora spezzo la frazione

1 - v^n+p

i

v^p -1

i

v^n+p - 1

i

v^p -1

i

Ho esplicitato il meno cambiando segno al numeratore del secondo termine dopo l'uguale
Il primo termine corrisponde al valore attuale di una rendita immediata posticipata di n+p periodi ed il secondo ad una rendita immediata posticipata di p periodi, cioe':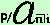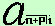

In questo modo negli esercizi potremo fare una sottrazione

Da notare che in pratica ho aggiunto ai periodi effettivi della rendita i periodi di differimento e quindi li ho tolti, in questo modo il valore della rendita resta invariato: nel disegno vedi in colori diversi:

In nero tutti i periodi
in rosso le rate originali

in blu le rate aggiunte: in questo modo le rate rosse e blu assieme danno

in verde le rate tolte

Se la rendita e' anticipata possiamo trasformarla in una rendita posticipata semplicemente togliendo un periodo al tempo del differimento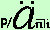

Cioe' ad esempio una rendita anticipata che inizi fra 5 anni si puo' considerare come una rendita posticipata che inizi fra 4 anni

Vediamo anche qui un semplice esempio
trovare il valore attuale di una rendita anticipata di periodo 10 anni e differita di 6 anni di rata 2000 € al tasso i = 0,02
Essendo la rendita anticipata cerco il valore attuale di una rendita posticipata differita di 5 anni
dati:
R = 2000 €
i = 0,02
n = 10
p = 5
n+p = 15
Utilizzo la formula

Cerco quindi sulle tavole "valore attuale della rendita unitaria immediata posticipata. valori di

" per i periodi 15 e 5

per i=0,02 e n=15 trovo il valore 12,84926350, quindi avro' il montante
12,84926350·2000 € = 25698,527 €
per i=0,02 e n=5 trovo il valore 4,71345951, quindi avro' il montante
4,71345951·2000 € = 9426,91902 €
Faccio la differenza
25698,527 - 9426,91902 = 16271,60798
che arrotondo a
16271,61 €